(Überarbeitet 14.2.2014)
In diesem Blog werden in der Hauptsache Ergebnisse analysiert und diskutiert, die mit Mitteln der Statistik erzielt worden sind. Statistik ist üblicherweise kein Schulfach. Auch in den Hochschulen wird Statistik nur denen vermittelt, die damit auch arbeiten müssen – und ist dann auch noch (reine subjektive Wertung!) sterbenslangweilig. Es erscheint daher sinnvoll, ein paar Begriffe zu klären. Dabei soll es bewusst nicht allzu sehr in die Tiefe gehen, auch die zum Teil recht aufwändige Mathematik wird nicht betrachtet. Es genügt, wenn sich der Leser am Ende unter den Begriffen etwas vorstellen kann und ihm klar ist, was die verschiedenen Größen aussagen.
Wer tiefer einsteigen will, sei auf die durchweg recht guten – wenn auch manchmal etwas schwer verständlichen – Artikel in der Wikipedia verwiesen. Wer sich intensiv mit Statistik befassen möchte, der sei auf die Lehrbücher [1], [2] verwiesen, wobei [2] sich dem Leser vielleicht etwas einfacher erschließt.
Normalverteilung
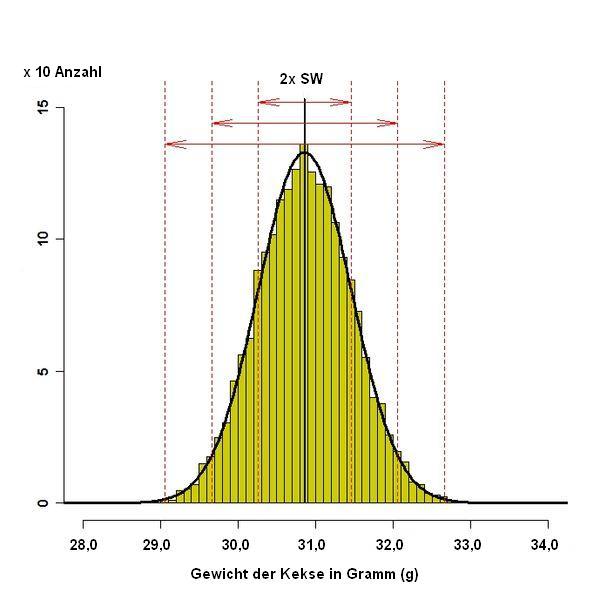
Die Statistik befasst sich mit der Analyse gleichartiger Daten, die in einer mehr oder weniger großen Anzahl vorliegen. Man teilt hierzu den gesamten Bereich, in dem die Zahlenwerte vorkommen, in mehrere Intervalle ein und zählt dann ab, wie viele Zahlenwerte in den jeweiligen Intervallen zu liegen kommen. Trägt man die ermittelten Häufigkeiten als Säulen auf, dann ergibt sich häufig – aber beileibe nicht immer – eine bestimmte Verteilung, wie z. B. hier im Bild:
Bei einer hinreichend großen Anzahl von Daten ergibt sich bei vielen Prozessen in Natur und Technik eine solche Verteilung, die durch die schwarze Kurve angenähert werden kann und als Normalverteilung oder auch Gauß-Verteilung, manchmal auch ihrer Form wegen als Glockenkurve bezeichnet wird.
Das Bild habe ich aus der Wikipedia deshalb ausgewählt, weil das Zustandekommen der Verteilung hier besonders gut zu erkennen ist. Allerdings wurde etwas ganz anderes dargestellt, dessen Erklärung hier zu aufwändig wäre und nur verwirren würde. Um eine möglichst bildhafte Vorstellung generieren zu können, wurde das Bild daher umgearbeitet und soll jetzt eine Versuchsreihe aus der Herstellung von Keksen darstellen.
Es wurde demnach eine Stichprobe von 2040 Kekse aus der laufenden Produktion entnommen und gewogen, was die im Bild dargestellte Kurve ergab. Man erkennt, dass die Kekse nicht alle gleich schwer waren, sondern, bedingt durch unterschiedliche Einflüsse, das Gewicht durchaus fühlbar streute. Solche Streuungen sind unvermeidlich, denn sowohl die Zutaten als auch die Herstellungsmaschinen sind den unterschiedlichsten Störgrößen ausgesetzt, beispielsweise kleinsten Schwankungen in den Eigenschaften der Rohstoffe, kleinsten Schwankungen beim Zumessen der Zutaten, in den Prozessgrößen (Ofentemperatur, tatsächliche Backzeit) und letztendlich in den Umgebungsbedingungen (Umgebungstemperatur, Luftfeuchtigkeit). Die Streuung wird umso kleiner sein, wenn man diese Bedingungen gut im Griff hat (Herstellung in klimatisierten Räumen auf vollautomatischen Maschinen) oder größer, wenn man sie nicht so genau einhalten kann, beispielsweise bei der handwerklichen Herstellung in einer Bäckerei.
Wenn eine Verteilung tatsächlich einer Normalverteilung entspricht, dann genügen zwei Daten (‚Parameter‘), um die Verteilung zu beschreiben: der Mittelwert und die Standardabweichung. Beide Werte sind mit Tabellenkalkulationsprogrammen (Excel) recht einfach aus vorliegenden Messwerten zu berechnen: Der Mittelwert ist der Durchschnitt aller Einzelwerte, in unserem Beispiel also die Summe des Gewichts aller Kekse dividiert durch deren Anzahl. Die Standardabweichung kann ebenfalls aus den Daten errechnet werden, wenn auch nicht mehr ganz so einfach. Für die im Bild dargestellte Verteilung beträgt der Mittelwert 30,87 g, die Standardabweichung wurde zu 0,6 g ermittelt.
Standardabweichung
Was bedeuten diese Zahlen aus dem vorigen Kapitel?
Bei einer Normalverteilung liegen rund zwei Drittel aller gemessenen Werte (genau 68,27 %) in einem Intervall von +/- der Standardabweichung um den Mittelwert. Dies ist im Bild der Bereich zwischen den beiden inneren roten Linien, am Doppelpfeil mit 2 x SW gekennzeichnet. Hier im Beispiel liegt das Gewicht von 1392 Keksen zwischen 30,27 und 31,47 g.
In dem doppelt so breiten Bereich von 2 x Standardabweichung um den Mittelwert liegen rund 95 % aller Messwerte (genau 95,45 %). Im Beispiel heißt das, dass 1947 Kekse zwischen 29,67 und 32,07 g gewogen haben. Im Bereich +/- 3 x Standardabweichung liegen schließlich fast alle Messwerte (genau 99,73 %), im Beispiel sind 2035 Kekse zwischen 28,47 und 32,67 g schwer.
Offenbar ist die Standardabweichung ein Maß für die Streuung. Wäre die Standardabweichung nur halb so groß, dann würden zum Beispiel 1392 Kekse zwischen 30,57 und 31,17 g wiegen anstelle der oben genannten 30,27 und 31,47 g. Die Kurve wäre wesentlich schmaler und spitzer.
Die Standardabweichung ist also eine Eigenschaft der Verteilung der Daten. Der Zahlenwert hängt nicht davon ab, wie groß der Umfang der Stichprobe ist. Die Verteilung selbst mag sich vielleicht ändern, je mehr Elemente betrachtet werden – der Mittelwert wird nach dem Messen von nur 5 Keksen ein anderer sein als nach dem Messen von 100, aber das liegt daran, dass sich die Verteilung in der Stichprobe ändert.
Wir halten fest: je kleiner die Standardabweichung, desto enger gruppieren sich die Messwerte um den Mittelwert. Prinzipiell gilt dies für jede Verteilung, nicht nur für die Normalverteilung. Für die Normalverteilung charakteristisch ist, dass die Standardabweichung, wie oben beschrieben, Bereiche abgrenzt, in denen ganz bestimmte Anteile der Daten liegen.
Vertrauensbereich
Wozu hat man den obigen Versuch mit den Keksen gemacht? Man möchte offenbar wissen, ob der Produktionsprozess das liefert, was geplant wurde. Dazu kann man alle produzierten Kekse wiegen, was bei einem Massenprodukt recht aufwändig wäre. Stattdessen entnimmt man eine mehr oder weniger große Menge als Stichprobe, untersucht diese, und nimmt an, dass es sich mit der Gesamtmenge (‚Grundgesamtheit‘) ähnlich verhalte wie mit der Stichprobe.
Das Ziehen der Stichprobe erfolgt aber zufällig, daher ist nicht unbedingt sicher, dass die Stichprobe auch genau der Grundgesamtheit entspricht. Generell gilt aber, je größer die Stichprobe ist, desto besser wird die Annäherung sein. Ein Maß dafür ist der Vertrauensbereich. Er gibt an, wie weit beispielsweise der Mittelwert der Grundgesamtheit von dem Mittelwert der Stichprobe abweichen kann. (Man könnte ebenfalls einen Vertrauensbereich für die Standardabweichung ermitteln.) Dieser Bereich kann aber kein fester Wert sein, sondern es kann nur ein Bereich angegeben werden, in dem der Mittelwert mit einer gewissen Wahrscheinlichkeit liegt. Üblich ist es, eine Wahrscheinlichkeit von 95 % zu Grunde zu legen. Mit einer Wahrscheinlichkeit von 5 % läge der Mittelwert der Grundgesamtheit dann außerhalb des angegebenen Vertrauensbereichs. (Hinweis: Diese Darstellung ist mathematisch gesehen nicht ganz korrekt, aber einprägsam und für den Zweck, den wir hier betreiben völlig ausrechend. Genaueres kann diesem Artikel in der Wikipedia antnommen werden.)
Für den Mittelwert der obigen Stichprobe lässt sich ein Vertrauensbereich von +/- 0,026 g errechnen. Das heißt, der Mittelwert des Gewichts der Kekse aus der gesamten Produktion liegt mit 95 % Wahrscheinlichkeit zwischen 30,87 – 0,026 g und 30,87 + 0,026 g, also zwischen 30,84 und 30,90 g.
Dieser vergleichsweise kleine Vertauensbereich kommt durch die extrem hohe Anzahl der Stichprobe zu Stande. Hätte man beispielsweise nur 1000 oder 100 Kekse als Stichprobe gewogen, dann wäre der Vertrauensbereich deutlich größer, nämlich 0,038 beziehungsweise 0,12 g. Der Vertrauensbereich für eine Verteilung ist, wie man sieht, außer von den Parametern der Verteilung selbst (Mittelwert, Standardabweichung) auch vom Umfang der Stichprobe abhängig. Je größer die Stichprobe, desto sicherer stimmt sie mit der Grundgesamtheit überein und desto schmaler der Vertrauensbereich.
Nochmals deutlich zum Vergleich:
Die Standardabweichung ist ein Maß dafür, wie eng die Messwerte an einer Stichprobe um den Mittelwert streuen, der Vertrauensbereich ist ein Maß dafür, wie gut die Stichprobe die Grundgesamtheit abbildet.
Anmerkung:
Bei der Berechnung des Vertrauensbereichs (und einiger anderer Werte) kommt eine Größe vor, die Standardfehler genannt wird. Dies ist die Standardabweichung dividiert durch die Wurzel aus der Anzahl der Objekte in der Stichprobe. Da diese Zahl erheblich kleiner ist als die Standardabweichung, wird sie gerne in den Grafiken der Veröffentlichungen verwendet, denn dann kann es so aussehen, als würden sich die Wertebereiche zweier Verteilungen nicht überlappen. Ich sehe darin allerdings nur eine Schönfärberei der Messergebnisse, denn eine Abschätzung der Streuung ist aus diesem Wert alleine nicht möglich.
Vertrauensbereich und Signifikanz
In den Untersuchungen, die hier im Blog analysiert werden, werden normalerweise die Ergebnisse an zwei Gruppen miteinander verglichen, beispielsweise die Ergebnisse, die sich bei homöopathischer Behandlung ergaben, mit den Ergebnissen einer anderen Gruppe, die nur Placebo erhielt. Einige Grundgedanken zur Signifikanz wurden bereits hier dargelegt. Daher sei an dieser Stelle nur daran erinnert, dass die statistische Signifikanz ein Maß dafür ist, dass ein Ergebnis nicht alleine durch Zufall entstanden sein kann. Mit dem Begriff des Vertrauensbereichs kann man aber noch einen weiteren Effekt anschaulich machen.
Wenn die Daten zweier Gruppen signifikant verschieden sind, dann sind sie sehr wahrscheinlich nicht durch Zufall zu Stande gekommen. Das heißt aber auch, dass sich die Vertrauensbereiche beider Verteilungen nicht überlappen. Dies ist möglich, wenn die Mittelwerte beider Gruppen weit auseinander liegen oder die Vertrauensbereiche sehr schmal sind. Letzteres kann wie oben ausgeführt dadurch erreicht werden, dass die Anzahl der Teilnehmer in den Gruppen hinreichend groß ist. Bildlich ist dann erreicht, dass sich die Ergebnisse der beiden Gruppen zwar nur wenig unterscheiden, vielleicht sogar recht stark streuen, aber man sehr sicher sein kann, dass dies auch in den zu Grunde liegenden Grundgesamtheiten genau so der Fall ist.
Daraus kann gefolgert werden, dass eine statistische Signifikanz nicht unbedingt eine Aussage dazu macht, wie weit die Daten auseinanderliegen. Es kann also durchaus sein, dass
-
die Ergebnisse zweier Gruppen stark streuen, das heißt, dass die Standardabweichung relativ groß ist
-
die zugehörigen Vertrauensbereiche aber wegen der hohen Zahl der Teilnehmer recht schmal sein können
-
und daher auch bei kleinen Unterschieden trotz starker Streuungen ein signifikantes Ergebnis erzielt wird.
Zur Illustration:
Nehmen wir an, der obige Versuch wäre mit einer anderen gleich großen Stichprobe wiederholt worden und man hätte einen Mittelwert von 31,00 g anstelle 30,87 g gefunden. Wenn beide Stichproben über 2000 Kekse umfasst hätten, dann wäre das Ergebnis signifikant, denn die Vertrauensbereiche überlappen sich nicht (30,87 + 0,026 = 30,90 und 31,00- 0,026 = 30,97). Dies würde auf eine systematische Änderung hindeuten, entweder der Störgrößen oder irgendwo am Produktionsprozess.
Wären die gleichen Verteilungen bei zwei Untersuchungen an jeweils nur 100 Keksen zu Stande gekommen, dann wäre das Ergebnis nicht signifikant, da sich die Vertrauensbereiche überlappen (30,87 + 0,12 = 30,99; 31,00 – 0,12 = 30,88). Das Ergebnis kann durch reinen Zufall entstanden sein, etwa weil zufällig mehr schwere Kekse in die Stichprobe geraten sind, was sich durch eine größere Zahl in der Stichprobe wahrscheinlich ausgleichen würde.
Effektstärke
Da auch kleine Unterschiede signifikant sein können, ist die Signifikanz als Aussage des Ergebnisses noch relativ unbefriedigend. Dafür wird oft die Effektstärke benutzt, die den Unterschied zwischen den Mittelwerten zweier Verteilungen mit der Standardabweichung, also mit deren Streuung, vergleicht. Dazu wird der Unterschied der Mittelwerte durch den Mittelwert der Standardabweichungen dividiert. Eine Effektsstärke von 1 bedeutet also, dass die beiden Mittelwerte um eine Standardabweichung auseinander liegen.
Es wird angegeben, dass eine Effektstärke von 0,1 ein schwacher Effekt, 0,5 ein mittlerer Effekt und 0,8 ein starker Effekt sei. Dies mag eine rein statistisch-theoretisch brauchbare Einteilung sein, ich selbst teile diese Ansicht aber eher nicht. Selbst eine Effektstärke von 1,0 führt dazu, dass sich etwa ein Drittel der Daten überlappt, rund 10 % sogar über den Mittelwert der jeweils anderen Verteilung herausragen.
Im obigen Fall wäre die Effektstärke (31,00 – 30,87) / 0,60 = 0,22, also auf jeden Fall recht gering.
Aus meiner Sicht ist es aber viel wesentlicher, ob der Unterschied auch relevant ist, das heißt irgendwie fühlbar ist. Das ist aber auch davon abhängig, was man eigentlich betrachtet. Wenn der Produktionsprozess betrachtet wird, dann könnte in dem obigen Beispiel eine Änderung um 0,13 g schon wesentlich dafür sein, dass sich etwas am Prozess verändert, beispielsweise ein Werkzeug anfängt zu verschleißen oder eine andere Prozessstörung sich ankündigt. Erfolgt die Betrachtung aber im Hinblick darauf, was diese Kekse in dem Menschen, der sie isst, anrichten, dann sind 0,1 g gar nichts, ja sogar 1 g wäre noch völlig bedeutungslos. Zugegeben, dann würde man nicht das Geld für so große Stichproben aufwenden, aber diese Betrachtung soll ja nur den grundsätzlichen Sachverhalt verdeutlichen.
Messunsicherheit
Ein wesentliches Kriterium zur Beurteilung der Aussagekraft ist es aber auf jeden Fall, ob die vorgefundenen Unterschiede noch innerhalb der Unsicherheiten der Messung liegen oder nicht.
Dass Messungen grundsätzlich mit Messfehlern behaftet sind, ist vielleicht noch einleuchtend, aber Messtechnik ist ein Gebiet, das dem Laien normalerweise gar nicht zugänglich ist. Man schaut gerne auf die Anzeige, zählt wie viele Stellen das Display anzeigen kann und hält dies dann für die Messgenauigkeit – was leider nicht zutrifft. Im Detail wäre es wohl angemessen, dem Thema einen eigenen Blogbeitrag zu widmen, was wahrscheinlich auch irgendwann einmal erfolgen wird.
Für jetzt muss allerdings einfach die Feststellung genügen, dass jede Messung durch Störgrößen mehr oder weniger stark verfälscht wird. Das heißt, dass es selbst bei einer unveränderten Messgröße (das, was man messen will, also z. B. das Körpergewicht) zu unterschiedlichen Messergebnissen kommen kann. Man denke einmal an den Einfluss auf das Wiegeergebnis, wie man auf der Waage steht (jeder Übergewichtige kennt die Suche nach der optimalen Position!). Das heißt aber auch, dass Messergebnisse nur dann sicher auf eine Änderung der Messgröße schließen lassen, wenn sie sich um mehr als die Messunsicherheit unterscheiden. Die Messunsicherheit legt also die Auflösung des Messsystems fest, kleinere Unterschiede als die Messunsicherheit kann man nicht unterscheiden.
Bleiben wir beim Körpergewicht. Wenn Sie sich täglich wiegen, werden Sie merken, dass Ihr Gewicht sich von Tag zu Tag um vielleicht ein ganzes Kilo nach oben oder unten bewegen kann, selbst wenn Sie sich jeweils nach dem Aufstehen und dem Gang zur Toilette wiegen. Soweit ich weiß, ist dies vom Wasserhaushalt abhängig, was, wie viel und wann Sie am Abend zuvor gegessen haben, wie viel Sie am Tag zuvor getrunken haben, wie viel Salz Sie aufgenommen haben und vieles mehr. Einen Erfolg eventueller Bemühungen, das Gewicht zu reduzieren, können Sie erst dann sicher feststellen, wenn die Anzeige aus dem Bereich der normalen täglichen Schwankung herauskommt.
Ein Problem der Messunsicherheit und der damit verbundenen Messauflösung ist, dass man mit keinem Trick der Welt ein genaueres Messergebnis erzielen kann als durch die Messauflösung vorgegeben. Diese Tatsache ist auch offensichtlich manchen Wissenschaftlern nicht bewusst. Man kann die Messunsicherheit selbst verringern, indem man die Bedingungen genau kontrolliert, aber diese ist und bleibt eine Grenze für die Genauigkeit eines Messergebnisses. Man kann zwar durchaus mit Mitteln der Statistik aus einer Vielzahl von Messungen Zahlenwerte ermitteln, die genauer zu sein scheinen, als die Auflösung des Messystems, aber der Einzelwert ist nicht genauer bestimmbar. Wenn man aber zwei solcher statistisch zustande gekommene Ergebnisse miteinander vergleicht und der Unterschied ist kleiner als die Auflösung – kann man den rechnerischen Unterschied in der Realität nicht nachvollziehen.
Ein zugegeben etwas konstruiertes Beispiel:
Nehmen Sie an, Sie haben eine Diät zur sanften Gewichtsreduktion erfunden. Sie machen den Versuch an einen großen Zahl von Probanden Ihrer Zielgruppe, indem Sie eine Ausgangsmessung machen, dann Ihre Kur verabreichen und eine Woche später wieder messen. Nehmen wir an Sie hätten nur ein Messystem zur Verfügung, dass das Gewicht Ihrer Probanden nur auf ein Kilogramm genau ermitteln kann, indem die weiteren Ziffern einfach abgeschnitten werden. Aus verschiedenen Gründen ist eine Messung des Körpergewichts mittels handelsüblicher Personenwaagen in der Tat nicht genauer, obwohl tatsächlich noch Zwischenwerte angezeigt werden. Aber, um dies jetzt nicht weiter auswalzen zu müssen, stellen Sie sich eine Waage vor, die nur Kilogramm anzeigen kann.
Wenn man die Ausgangsmessung durchführt und dann den Mittelwert (‚Erwartungswert‘)bildet, dann kann man durchaus auch Zahlenwerte errechnen, die im Grammbereich liegen. Nach dem Zentralen Grenzwertsatz wird dieser Zwischenwert wahrscheinlich auch immer besser dem tatsächlichen Mittelwert in der Gesamtheit aller Menschen Ihrer Zielgruppe entsprechen, je mehr Probanden Sie verpflichtet haben.
Nun geben Sie ihr Mittel und machen eine Woche später die gleiche Messung. Auch hier können Sie wieder einen Zwischenwert bestimmen, der bei hinreichend hoher Anzahl von Teilnehmern das Ergebnis repräsentiert, wie die Menschen Ihrer Zielgruppe wahrscheinlich reagieren. Wenn man das Ergebnis genauer errechnen kann als es der Messauflösung entspricht, dann ist es auch möglich, dass es Unterschiede in den Durchschnittswerten gibt, die kleiner sind als die Auflösung des Messystems. Es könnte sich zum BEispiel ergeben, dass der Durchschnitt der Ausgangsmessung bei 89,7 kg lag, jetzt liegt der Wert bei 89,3 kg.
Das mag ja rechnerisch ein ganz toller Erfolg sein, aber der Durchschnittproband merkt den Unterschied nicht. Da die Waage einfach die Gramm-Stellen abschneidet, bekommt er vor wie nach 89 kg als sein Körpergewicht angezeigt. Für ihn hat sich subjektiv nichts geändert, der Vorteil ist, obwohl in der Summe der Probanden vielleicht fühlbar, für den einzelnen Nutzer irrelevant (‚Und kannnst Du’s nicht messen, dann kannst Du’s vergessen!‘). Natürlich kann es in dieser Konstellation einzelne Nutzer geben, die einen ganz erheblichen Vorteil erzielen, dem werden aber auch solche gegenüberstehen, die einen Nachteil zu verzeichnen haben.
Aus diesen Überlegungen heraus erscheint es mir gerechtfertigt, Unterschiede der Gruppenergebnisse klinischer Stuien, die unterhalb der Auflösung des Messsystems liegen, als irrelevant zu betrachten. In den Augen des Nutzers kann man die Nachkommastellen in unserem Beispiel auch würfeln. Mehr Bedeutung aht es für ihn nicht.
Gut, in dem hier betrachteten Fall wird die Werbung des Rest machen müssen, um weitere emotionale Vorteile mit dem Produkt zu verbinden, aber im Hinblick auf das Primärziel bringt das nichts, zumindest nichts Messbares.
Wenn mit den Messwerten noch Kennwerte ermittelt werden, insbesondere wenn dabei zwei oder mehr Messwerte verknüpft werden, gibt es noch den Effekt der Fehlerfortpflanzung. Der Vollständigkeit halber soll hier ein klassisches Beispiel dargestellt werden: Wie groß ist der Flächeninhalt eines Quadrats mit 2,5 m Seitenlänge? Jeder nennt, gegebenenfalls mit etwas Rechnen, 6,25 m² als Ergebnis, vermeintlich mit einer Genauigkeit von drei Stellen, obwohl die Eingangsdaten nur eine Genauigkeit von zwei Stellen aufwiesen (ich sagte 2,5, nicht 2,50!). Nach allgemeiner Übereinkunft ist 2,5 m irgendein Wert zwischen 2,45 m und 2,55 m. Der Flächeninhalt kann also zwischen 2,45 x 2,45 = 6,00 m² und 2,55 x 2,55 = 6,50 m² liegen. In der Genauigkeit ist nicht eine Stelle gewonnen worden, sondern eine ging verloren! Die zweite Stelle kann irgendwo zwischen 0 und 5 liegen, die Dritte ist vollends Lotterie. Als Faustregel fordert man daher in der Messtechnik, dass die Auflösung des Messsystems etwa eine Zehnerpotenz besser sein muss als die gewünschte Genauigkeit des Ergebnisses.
Wegen der Einprägsamkeit noch eine Tabelle zur Fehlerfortpflanzung schon bei den Grundrechenarten. Die Tabelle zeigt die extremen Ergebnisse der mit den Zahlen 4 und 5 ausführbaren Grundrechenoperationen, wenn die Zahlen um jeweils 0,5 schwanken, ‚4‘ also ein Wert zwischen 3,5 und 4,5 ist und ‚5‘ ebenso zwischen 4,5 und 5,5.
| Operation | Kleinstwert | Größtwert |
|---|---|---|
| Addition 5 + 4 | 8 | 10 |
| Subtraktion 5 - 4 | 0 | 2 |
| Multiplikation 5 x 4 | 15,75 | 24,75 |
| Division 5 / 4 | 1,0 | 1,57 |
Ich finde es jedenfalls immer wieder erstaunlich, wie schnell sich Ungenauigkeiten bei Rechenoperationen vergrößern.
Jetzt die Kurve zurück auf die Statistik: Die Arithmetik kann vortäuschen, dass die Ergebnisse aussehen, als seien sie genauer als von der Auflösung des Messsystems vorgegeben, das ist aber bloße Arithmetik und nicht real. Daher ist ein Ergebnis, also beispielsweise der Unterschied der Messwerte zweier Gruppen, völlig ohne Aussage, wenn er geringer ist als die Messunsicherheit – die man allerdings eventuell schätzen muss. Aus mir nicht nachvollziehbaren Gründen wird das Thema der Messauflösung in den allermeisten Veröffentlichungen nicht diskutiert. Da mag das Ergebnis noch so signifikant sein, wenn die Messgenauigkeit das nicht hergibt, ist das Ergebnis nicht zu gebrauchen.
Anwendung auf ein Beispiel
Im Licht dieser Ausführungen können wir uns nochmal das Ergebnis der Analyse der Krebsstudie von Rostock betrachten. Man hatte dort ermittelt, dass der Index der Lebensqualität für die homöopathisch behandelten Patienten von 75,6 auf 81,1 Punkte angestiegen war, der der konventionell behandelten Patienten von 75,3 nur auf 76,6 (nehmen wir mal die Zahlen, wie sie im Text der Arbeit zitiert werden), die ganze Entwicklung spielte sich also in einem Bereich von noch nicht einmal 6 Punkten ab. Die Standardabweichung betrug jeweils rund 15 bis 16 Punkte, die Auflösung des Messverfahrens wurde von seinem Erfinder mit 3 bis 7 Punkten angegeben.
Ohne Zweifel zeigen die Ergebnisse in den einzelnen Gruppen eine starke Streuung, aber solche Ergebnisse gibt es. Die Effektstärke ist mit ca. 0,35 nicht gerade hoch. Allerdings liegt aufgrund der vergleichsweise hohen Teilnehmerzahl der Vertrauensbereich bei nur rund zwei Punkten. Das heißt, die Stichproben geben mit großer Sicherheit die Verhältnisse in der Grundgesamtheit wieder. Damit sind die Unterschiede statistisch signifikant. Aber das ist rein die Mathematik, die nicht wissen kann, auf welch dubiose Art und Weise die Eingangsdaten zustande gekommen sind. Auch hier gilt die Regel Unsinn rein – Unsinn raus.
Wenn die Ergebnisse mit einem Messverfahren ermittelt worden wären, das eine Auflösung von etwa 0,5 Punkten gehabt hätte (etwa ein Zehntel des Datenbereichs), dann könnte man das sogar glauben. Unser Ansatzpunkt der Kritik ist aber gerade die Genauigkeit der Datenerfassung. Das Auswerteprogramm für die Daten macht sich keine Gedanken darüber, dass neben jedem Zahlenwert, der eingetippt wird, eigentlich die Angabe ‚+/- 3 bis 7 Punkte‘ stehen müsste, und dass es merkwürdig ist, dass Krebskranke hierzulande in den Wirren der Akutbehandlung eine nur wenig schlechtere Lebensqualität verzeichnen als die durchschnittliche Bevölkerung in den USA.
Natürlich stimmt diese kurze Analyse überhaupt nur, wenn die Messergebnisse der Studie tatsächlich jeweils eine Normalverteilung ergeben. Wenn nicht, können noch sehr viele weitere Ungenauigkeiten aufgetreten sein, die wir rechnerisch nicht erfassen können. Darüber schweigen sich aber die Verfasser aus.
Zusammenfassung:
-
Die Standardabweichung ist eine Eigenschaft der Verteilung der Daten und sagt etwas über deren Streuung.
-
Der Vertrauensbereich sagt etwas darüber aus, wie gut die Stichprobe die Grundgesamtheit wiedergibt.
-
Die statistische Signifikanz kann man als Maß deuten, wie weit sich die Vertrauensbereiche zweier Verteilungen überlappen.
-
Die Effektstärke vergleicht den Unterschied zwischen zwei Verteilungen mit deren Standardabweichung, ist also ein Maß dafür, wie gut sich die Ergebnisse voneinander unterscheiden.
-
Die Messunsicherheit ist ein Maß für die Genauigkeit der Daten, die in die Betrachtung eingeflossen sind. Dies ist eine nicht zu überwindende Grenze für die Präzision des Ergebnisses.
Bildnachweis:
Quelle: Wikimedia, UncertFIGURE1.jpg Autor: Rb88guy, Modifikation: Verfasser
Weiterführende Literatur:
[1] Fahrmeir L, Künstler R, Pigeot I, Tutz G. Statistik – Der Weg zur Datenanalyse. Springer Verlag, 2011. ISBN: 978-3-642-01938-8
[2] Bühner M, Ziegler M. Statistik für Psychologen und Sozialwissenschaftler. Pearson GmbH, München 2009. ISBN: 978-3-8273-7274-1








Pingback: Heels Schwindelpräparate @ gwup | die skeptiker
Herzlichen Dank für diese zusammenfassende Darstellung einiger wichtiger Begriffe aus der Statistik, die einem immer wieder begegnen, wenn man sich mit empirischen Studien auseinandersetzt.