Ich freue mich sehr, diesen Gastbeitrag von Ute Parsch veröffentlichen zu können. Darin wird ein Thema behandelt, eine Arbeit über die quantenmechanische Modellbildung der Potenzierung, das ziemlich an der Grenze meiner eigenen Fachkompetenz liegt, allerdings von der falschen Seite her. Es sei darauf hingewiesen, dass ich jederzeit bereit bin, Gastbeiträge, die zum Thema des Blogs passen, auf diesen Seiten zu veröffentlichen. Wie hier ersichtlich, kann das Thema Homöopathie dadurch umfassender behandelt werden.
Norbert Aust
Ute Parsch:
Diskussion zu ‚Quasi-Quantum Model of Potentization‘ von Marcin Molski
Ein Grundproblem für die Befürworter der Homöopathie ist, dass es kein mit den Erkenntnissen der Naturwissenschaften verträgliches Erklärungsmodell für die Wirkweise einer homöopathischen Arznei gibt. Hahnemann selbst sprach von einer „fast geistigen Kraft der Arzneien“. Es ist der Homöopathie jedoch nicht gelungen, diese Formulierung in einen plausiblen wissenschaftlichen Kontext zu stellen. Einen neuen Versuch in diese Richtung unternimmt Marcin Molski, Professor an der chemischen Fakultät der Adam Mickiewicz Universität in Posen, in seinem Artikel „Quasi-Quantum Model of Potentization“.
Das Paper wurde bereits 2009 auf dem arXiv-Dokumentenserver unter „allgemeiner Physik“ abgelegt (arXiv:0911.4514 [physics.gen-ph]; Link zum Volltext), allerdings erst im Oktober 2011 in der Zeitschrift Homeopathy veröffentlicht. (Homeopathy, Volume 100, Issue 4, Pages 259-263, October 2011, Link). Einen Vortrag zu den wesentlichen Aussagen hat Molski auf dem Kongress der International Homeopathic Medical League 2009 gehalten.
Es handelt sich also bei Molskis Artikel nicht um eine medizinische Studie, sondern um eine rein theoretische Arbeit im Rahmen der Physik. Für eine Beurteilung der vorgestellten Argumente ist es dementsprechend allein ausschlaggebend, ob diese aus der Sicht der Physik korrekt und stichhaltig sind.
Ohne jetzt groß auf die Formeln blicken zu wollen, ist Molskis Argumentation die Folgende:
Beim Potenzieren nimmt die Konzentration des Wirkstoffes in einer homöopathischen Arznei mit jedem Potenzierungsschritt exponentiell ab. Entsprechend nähert sich die Konzentration des Lösungsmittels mit jedem Schritt exponentiell der 100%-Marke. Da man in etwa für jeden Potenzierungsschritt gleich lang arbeitet, kann man diesen Konzentrationszuwachs des Lösungsmittels auch als eine Funktion der Zeit auffassen und schreiben
S(t) = 1 – exp(-at) wobei a = ln10/t0;
t0 ist die Zeitspanne, die man für einen Potenzierungsschritt (D-Potenzen) benötigt, also eine Konstante. Damit ist auch a eine Konstante. Mit seiner Interpretation der Potenzierung als Funktion über die Zeit, hat Molski also einen sehr einfachen mathematischen Zusammenhang für die Konzentrationszunahme des Lösungsmittels S(t) gefunden.
Da Molski nun eine Funktion der Zeit vor sich hat, kann er diese auch zweimal nach der Zeit differenzieren und erhält formal korrekt die folgende Differentialgleichung
Aus diesen Gleichungen zieht Molski seine zentrale Schlussfolgerung: (Frei übersetzt)
„Die Funktion S(t) ist ein Spezialfall der West-Brown-Enquist Kurve, die das ontogenetische Wachstum beschreibt. Deshalb ähnelt der Konzentrationszuwachs des Lösungsmittels während des Potenzierens dem Wachsen biologischer Systeme.“
Sowie:
„Man kann zeigen, dass diese Differentialgleichung ein Spezialfall der nicht lokalen Horodecki-Feinberg-Gleichung für das zeitabhängige Hulthèn Potential im Falle der kritischen Abschirmung ist. Dieses Ergebnis bedeutet, dass der Prozess der Konzentrationszunahme der Lösungsmittelmoleküle während der Zubereitung einer homöopathischen Arznei in die Klasse der Quasiquantenphänomene gehört.“
Die letzten Sätze muss man vermutlich mehrmals lesen, sind sie doch reichlich mit recht speziellen Fachbegriffen aus verschiedenen Fachrichtungen gespickt. Daher Schritt für Schritt betrachtet und einfacher formuliert: Wie sinnvoll sind Molskis Folgerungen?
Streng genommen beschreiben Molskis Gleichungen nicht die Konzentration des Lösungsmittels und ihre Veränderung, sondern die Wahrscheinlichkeit, in der Mischung zu einem bestimmten Zeitpunkt (bzw. nach einem bestimmten Potenzierungsschritt) nur noch Lösungsmittelmoleküle zu finden. Darin liegt aber sicher nicht das Hauptproblem in Molskis Argumentation, lassen wir ihm seine Wortwahl. Mathematisch korrekt sind die Gleichungen.
Molski zeigt zunächst, dass die Konzentration des Lösungsmittels beim Potenzieren zunimmt und zwar genau entgegengesetzt zur Abnahme der Wirkstoffkonzentration. Das ist bei allen Verdünnungsprozessen so. Dass beim Potenzieren diese Änderungen mit Exponentialfunktionen beschrieben werden können, liegt einfach am Verfahren, immer in gleichen Schritten zu verdünnen.
Viele natürliche Vorgänge können mit Exponentialfunktionen beschrieben werden. Dieser mathematisch eigentlich sehr einfache Zusammenhang beschreibt Systeme immer dann, wenn die Änderungsrate einer physikalischen Größe (zum Beispiel die Menge eines Stoffes) direkt proportional zur Größe selbst ist. Es ist also nicht wirklich überraschend, dass Molski exponentielle Zusammenhänge auch in anderem Kontext findet.
Nun folgert Molski aus der Tatsache, dass er die zeitliche Änderung der Lösungsmittelkonzentration in derselben Weise mathematisch darstellen und differenzieren kann wie andere physikalische Größen, dass zu diesen anderen physikalischen Größen ein logischer Zusammenhang bestünde. Zur Beurteilung dieser Schlussfolgerung kommt es zunächst gar nicht darauf an, mit welchem Phänomen Molski die logische Verknüpfung über die Gleichheit der Formel ableitet, sondern nur um die Frage, ob dieser Schritt physikalisch überhaupt richtig ist.
Die zu stellende Frage ist also: Beruhen alle Phänomene, die sich mit denselben mathematischen Zusammenhängen darstellen lassen auch auf derselben Physik? Und die Antwort auf diese Frage ist: Nein. Die Beschreibbarkeit zweier Phänomene durch dieselbe mathematische Funktion stellt keinen logischen oder physikalischen Zusammenhang zwischen beiden Phänomenen dar. Molskis Schlussfolgerung ist falsch.
Um sich dies klar zu machen, genügen erheblich einfachere Beispiele.
Zum Beispiel wird in der Physik die gleichförmige Bewegung, also die Bewegung mit konstanter Geschwindigkeit durch die einfache Formel
s = v · t; mit s = zurückgelegter Weg; v = Geschwindigkeit, t = verstrichene Zeit
beschrieben. Ein einfacher linearer Zusammenhang. Solche linearen Zusammenhänge kennt man aber auch bei ganz anderen physikalischen Größen. Zum Beispiel gilt in einem einfachen Stromkreis mit einer einfachen Glühbirne konstanter Leistung
E = P · t; mit E = verbrauchte elektrische Energie, P = Leistung, t = verstrichene Zeit
Die verbrauchte elektrische Energie einer Glühbirne bestimmter Leistung hängt also in derselben Weise von der Zeit ab, wie der zurückgelegte Weg, wenn man sich mit konstanter Geschwindigkeit bewegt. Dennoch würde niemand auf die Idee kommen, deswegen die gleichförmige Bewegung logisch mit elektromagnetischen Phänomenen verknüpfen zu wollen. Das ist ganz offensichtlicher Unsinn. Genau diesen Schritt macht aber Molski, wenn er aus der Gleichheit der Formel für S(t) mit einer Formel für biologisches Wachstum irgendwelche logischen Analogien folgert.
Man könnte sich viele Beispiele dieser Art denken. Das Prinzip ist dasselbe: Gerade bei so einfachen Formeln wie linearen, quadratischen oder exponentiellen Zusammenhängen finden wir in der Natur verschiedenste Phänomene, die mit diesen Formeln beschrieben werden können. Dennoch steckt jeweils eine vollkommen andere Physik hinter den Beobachtungen.
Erst die Zuordnung der in einer Formel verwendeten Variablen zu realen, messbaren Größen stellt die mathematische Formel in einen physikalischen Kontext. Die Formel stellt dann aber nur eine Abhängigkeit der in ihr vorkommenden Größen voneinander dar, eine Verknüpfung zu anderen Phänomenen liefert sie nicht. Das gilt sowohl für die Formel selbst als auch für die zugrunde liegenden Differentialgleichungen.
Dass Molski also den oben dargestellten einfachen exponentiellen Zusammenhang für S(t) auch in Wachstumsraten biologischer Systeme findet, rückt das Potenzieren somit aus Sicht der Physik in keiner Weise in einen biologischen Kontext. Und auch durch die Tatsache, dass die zeitlichen Ableitungen dieser Gleichung sich formal mathematisch so umformen lassen, dass sie wie irgendeine quantenmechanische Gleichung aus komplett anderem Kontext dargestellt werden können, macht das Verdünnen nicht zu einem quantenmechanischen Vorgang.
Ein Professor für Chemie sollte das eigentlich wissen.
Die Willkürlichkeit der ausgewählten physikalischen Phänomene, bei denen hier eine formale Analogie fälschlich als physikalische Analogie dargestellt wird, wird deutlich, wenn man sich klar macht, dass daneben etliche weitere physikalische Vorgänge existieren, die auf denselben einfachen Zusammenhängen beruhen, die Molski aber in keiner Weise erwähnt.
Auch beim radioaktiven Zerfall sinkt die Anzahl der Mutterkerne beispielsweise exponentiell, die der Tochterkerne nimmt entsprechend zu. Zwischen Radioaktivität und Homöopathie möchte Molski jedoch keinen Zusammenhang herstellen, obwohl man hier die Argumentation über die Formeln ganz genauso führen könnte. Er versucht auch nicht einmal, eine Begründung für seine Auswahl zu geben.
Man findet aber sogar noch einfachere Prozesse in der Natur, die denselben Gleichungen genügen. Als Beispiel sei hier der freie Fall von Gegenständen mit Luftreibung genannt. Bei nicht zu großen Geschwindigkeiten ist die Luftreibung der Fallgeschwindigkeit proportional (Stokes-Gesetz), was dazu führt, dass sich ein Fallschirmspringer oder ein von einem Turm geworfener Basketball nach absolut derselben Formel exponentiell an ihre endgültige Fallgeschwindigkeit annähern wie Molskis S(t) an die 1. Ein Vergleich mit diesen Vorgängen zeigt jedoch deutlich, wie unsinnig Molskis Argumentation eigentlich ist. Es ist eben so, wie Markus Ronner gesagt hat: „Dass das Saxofon von Adolphe Sax stammt, ist noch kein Beweis dafür, dass das Telefon von Wilhelm Tell erfunden worden ist.“
Die Argumentation beruht fundamental auf einer physikalisch falschen Analogie und ist deshalb grundsätzlich nicht haltbar.
Da fällt es dann eigentlich gar nicht mehr ins Gewicht, dass Molski formal als Beleg seiner theoretischen Überlegungen Experimente anführt, die bereits ein Jahr vorher von einer Gruppe deutscher Homöopathen veröffentlicht wurden, bei denen allerdings keine der in Molskis Arbeit genannten Formeln überhaupt eine Rolle spielt – dafür aber sogenannte „holistische Photonen“ und „homöopathische Photonen“, die es in der Physik schlichtweg nicht gibt.
Und es ist eigentlich auch nur noch eine Randnotiz, dass Molskis Versuch, über diese falsche Analogie der homöopathischen Arznei eine „vital force“ zuzuordnen, schon aus Sicht der Biologie scheitert: Die West-Brown-Enquist Kurve beschreibt zwar das Wachstum verschiedener Organismen, jedoch entwickeln die Autoren ihre Formel aus elementaren biologischen Zellprozessen und führen hierzu keinerlei geheimnisvolle Kräfte in ihr Modell ein. “Here, we derive a general quantitative model based on fundamental principlesfor the allocation of metabolic energy between maintenance of existing tissue and the production of new biomass. We thus predict the parameters governing growth curves from basic cellular properties” („A general model for ontogenetic growth, Geoffrey B. West, James H. Brown& Brian J. Enquist , Nature413, 628-631 (11 October 2001), Link) Für West, Brown und Enquist spielen also Stoffwechselprozesse und Eigenschaften der Zelle eine Rolle, nicht aber eine „Lebenskraft“ á la Hahnemann. Selbst wenn die mathematische Analogie also S(t) in diesen biologischen Kontext rücken würde (was sie wie erläutert nicht tut), dann wäre das für Molskis Argumentation immer noch bedeutungslos, weil auch die ontogenetische Wachstumskurve, mit der er Analogie sucht, keine homöopathische Lebenskraft zur Erklärung des Wachstums benötigt.
Interessanter ist daher abschließend die Frage, ob Molskis Ergebnisse überhaupt zu den Aussagen der Homöopathie passen. Die hier vorgestellte Argumentation stellt die zeitliche Änderung der Konzentration des Lösungsmittels beim Verdünnen in den Mittelpunkt. („From the physical point of view, the precise numbers of shakings and dilutions in the given time sequences, or by an exact number of mixing (triturations) of a diluted medicinal substance is a kind of the homeopathic clock, which permits introduction of the potentization time and description of the time-change of the concentration of the solvent.”)
Aber passt das zu den Aussagen der Homöopathie? Nein, ganz offensichtlich nicht. Denn das exakt und vorschriftsmäßig durchgeführte Verschütteln wird bei Molski allein dazu benötigt, für jeden Potenzierungsschritt eine gleich lange Zeitspanne verstreichen zu lassen. Dabei geht seine „homöopathische Uhr“ recht ungenau, denn bei aller Sorgfalt dürfte es schwer sein, immer auf die Sekunde genau gleich lange für das Verschütteln und Umfüllen zu brauchen. Exakter wäre hier nach Molski, das Verschütteln ganz sein zu lassen – da es nach seiner Theorie ja ausschließlich dem Einhalten des Zeitschrittes dient – und eine Stoppuhr zu verwenden. Hahnemann hat jedoch ausdrücklich und ausführlich beschrieben, wie wichtig das Verschütteln für die Herstellung der Arzneien ist und wie, ja sogar auf welcher Unterlage es durchzuführen ist, um optimale Ergebnisse zu erzielen. Das macht nun in Molskis Bild keinerlei Sinn mehr, was er allerdings nicht diskutiert.
Homöopathische Mittel müssten also anders hergestellt werden, wenn Molskis Theorie zuträfe. Zwar bräuchte nicht mehr geschüttelt werden, dafür müsste jedoch die Zeitabfolge über den ganzen Potenzierungsprozess streng konstant bleiben. Nimmt man an, dass jeder Potenzierungsschritt 5 Minuten dauert – für das bisherige Schütteln und Verdünnen sicher keine unrealistische Zeitspanne – dann dauert die Herstellung einer D 200 Potenz möglichst exakt 1000 Minuten oder 16 Stunden 40 Minuten. Zur exakten Einhaltung dieser Zeit müssten die Mitarbeiter logischerweise auf Mittagspausen und Feierabend verzichten – oder es müsste im Schichtbetrieb gearbeitet werden, da der Prozess ja nicht einfach über Nacht unterbrochen werden könnte. Und natürlich stellt sich hier auch die Frage der Qualitätssicherung: Wie soll gewährleistet werden, dass der Zeitrhythmus bei der Fertigung eingehalten wurde? Sichtbar ist dies an den fertigen Globuli ja nicht.
Das ist aber nur der erste Punkt, der aus der Sicht der Homöopathie problematisch ist. Der zweite Punkt ist, dass es für Molskis Argumentation komplett unerheblich ist, welche Substanz denn nun verdünnt wird, denn er argumentiert ja ausschließlich über die Konzentrationsveränderungen des Lösungsmittels. Diese hängen jedoch nur vom Zeitverlauf des Verfahrens ab, nicht vom Ausgangsstoff. Nach Molski wäre es also komplett egal, welcher Stoff in der Urtinktur enthalten war. Auch auf diesen Punkt geht Molski mit keinem Wort ein.
Drittens kann auch Molskis Modell niemals, selbst wenn man alles andere außer Acht lassen würde, die Wirkung homöopathischer Hochpotenzen erklären, bei denen etliche Verdünnungsschritte durchgeführt wurden, ohne dass irgendetwas weiter verdünnt wurde. In der Praxis wird ab bestimmten Potenzen die Konzentration des Lösungsmittels nicht weiter zunehmen können, weil bereits kein einziges Wirkstoffmolekül mehr im vorherigen Schritt enthalten war. (Hier wird noch einmal wichtig, dass S(t) ja eigentlich nur die Wahrscheinlichkeit war, in der Mischung ausschließlich Lösungsmittelmoleküle zu finden.) Molskis Formeln können diesen Fall eigentlich nicht mehr beschreiben, weil sie das Erreichen dieses Zustandes als Grenzwert nach unendlicher Zeit darstellen. Beim realen Verdünnen mit geringen Stoffmengen läuft man jedoch in endlicher Zeit nach endlich vielen Schritten in diesen Fall. Damit könnte man aus Molskis Formeln niemals argumentieren, dass Hochpotenzen eine immer größere Wirkung haben. Auch das ist aber eine Kernaussage der Homöopathie.
Jeder Homöopath würde daher heftig gegen Molskis Erklärungsansatz protestieren – wenn es nicht so schön wäre, dass es wieder einmal einen „Beweis“ für die Homöopathie gibt. Aus Sicht der Physik kann man nur sagen, dass die hier vorgestellte Argumentation grundlegend falsch ist. Und selbst wenn sie gültig wäre, könnte sie die Homöopathie bei genauer Betrachtung nicht erklären. Dies fällt den meisten Lesern jedoch nicht auf, weil Molskis Arbeit mit Fachausdrücken nur so gespickt ist und dadurch wissenschaftlicher wirkt, als sie es tatsächlich ist.
Zur Person der Autorin:
 Mein Name ist Ute Parsch, ich bin 46 Jahre alt und wohne aktuell in München, stamme aber aus Franken. Nach dem Abitur habe ich an der Friedrich Alexander Universität in Erlangen Physik studiert und 1992 im Fachbereich Astrophysik mein Diplom erworben. Danach verließ ich die Universität in Richtung Siemens und war dort im Systemtest für Fehlersuche im Bereich der Telefongebührensoftware zuständig. Nach der Geburt meines Sohnes musste ich allerdings meine berufliche Tätigkeit unterbrechen.
Für alternative Medizin und Homöopathie im Speziellen begann ich mich zu interessieren, weil mir für meinen Sohn wiederholt sowohl von Bekannten als auch von Apothekern entsprechende Mittel empfohlen wurden, die vorgebrachten Argumente oder dargestellten Wirkmechanismen aber stets mit meinen naturwissenschaftlichen Kenntnissen im Widerspruch lagen. In dieser Überzeugung hat mich bisher auch das umfangreiche Material an Büchern und Studien, die ich bisher zu diesem Thema gelesen habe, immer wieder bestätigt.
Mein Name ist Ute Parsch, ich bin 46 Jahre alt und wohne aktuell in München, stamme aber aus Franken. Nach dem Abitur habe ich an der Friedrich Alexander Universität in Erlangen Physik studiert und 1992 im Fachbereich Astrophysik mein Diplom erworben. Danach verließ ich die Universität in Richtung Siemens und war dort im Systemtest für Fehlersuche im Bereich der Telefongebührensoftware zuständig. Nach der Geburt meines Sohnes musste ich allerdings meine berufliche Tätigkeit unterbrechen.
Für alternative Medizin und Homöopathie im Speziellen begann ich mich zu interessieren, weil mir für meinen Sohn wiederholt sowohl von Bekannten als auch von Apothekern entsprechende Mittel empfohlen wurden, die vorgebrachten Argumente oder dargestellten Wirkmechanismen aber stets mit meinen naturwissenschaftlichen Kenntnissen im Widerspruch lagen. In dieser Überzeugung hat mich bisher auch das umfangreiche Material an Büchern und Studien, die ich bisher zu diesem Thema gelesen habe, immer wieder bestätigt.

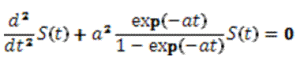







Pingback: „Unplausibel, irreführend“: Homöopathiekritik in tiermedizinischem Fachjournal | gwup | die skeptiker
Pingback: VT0100: Pharma-Meute instrumentalisiert GWUPS | FSMoSophica
Hätte Herr Molski sich ein Beispiel an Frau Parsch genommen, und hätte seine Ausführungen für Laien nachvollziehbar formuliert, wäre die beabsichtigte Wirkung seines Artikels, beim Leser den von Stanley Milgram sogenannten Agens-Zustand bei Akzeptieren von Autoritäten auszulösen, nicht erreicht worden. 😉
Grüße,
Martin Kiechle
Pingback: Homöopathie und die Medien @ gwup | die skeptiker
Pingback: Mond und Schlafstörungen @ gwup | die skeptiker
Pingback: Homöopathie: Studiendesign via Verallgemeinerter Quantentheorie? – Kritisch gedacht
Ganz kurz dachte ich auch an eine kleine Neuauflage der Sokal-Affäre, die bekanntlich nicht an einem ersten April stattgefunden hat, aber nach kurzer Recherche musste diese Hoffnung aufgegeben werden.
Die Logik, aus der Abwesenheit des Planckschen Wirkungsquantums h in einer Formel auf die Anwendbarkeit der schwachen Quantentheorie zu schließen, ist das absolute Highlight aus Molskis Paper. Vielen Dank für diesen Hinweis!
Belassen wir es aber dabei. Wie Frau Parsch und Herr Aust schon geschrieben haben, ist es ab einem gewissen Grad nur noch Zeitverschwendung, sich mit weiteren Argumenten en detail zu beschäftigen. Oder es zeugt von einem sehr seltsamen Sinn für Humor.
Hallo Herr Leick,
vielen Dank für diesen Kommentar. „Billiger Trick“ war genau der Gedanke, der mir an der entsprechenden Stelle im Paper auch durch den Kopf ging, was Ihrer Formulierung „Taschenspielertrick“ doch sehr nahe kommt.
Ich habe mich dann allerdings darauf beschränkt, dies nur in dem dezenten Ausdruck „erhält formal korrekt“ einfließen zu lassen – „formal korrekt“ im Sinne von „richtig gerechnet, aber auch nicht mehr“. Es erschien mir sehr aufwendig, hier das logische Problem einem Leser klarzumachen, der noch nie mit Differentialgleichungen gearbeitet hat, weshalb ich letztlich darauf verzichtet habe. Es gab einfacher darstellbare Ansätze, die Argumentation im Paper als unhaltbar zu entlarven. Gerade deshalb freue ich mich jetzt aber, dass es durch Ihren Kommentar doch noch erwähnt wird.
Man könnte noch erheblich mehr Einzelaussagen in Molskis Paper unter die Lupe nehmen. Man könnte die völlig unbegründete Bandbreite der doch recht speziellen Effekte, aus denen er seine Formeln klaut, noch besser beleuchten (man möchte fast von argumentativen „special effects“ sprechen…). Allein wie er aus der Tatsache, dass das Planck’sche Wirkungsquantum nicht in der Differentialgleichung vorkommt (woher denn auch?) und dass S(t) als Wahrscheinlichkeitsaussagen interpretiert werden kann (das ist von vorneherein so), auf die schwache Quantenmechanik von Atmanspacher kommt, verdient eigentlich eine Besprechung. Das Ganze wirkt einfach nur noch „gewollt“ (zumal ja gerade die Interpretation der Zustände als Wahrscheinlichkeiten in der schwachen Quantenmechanik fehlt).
Man könnte also eigentlich jedes Detail zerpflücken. Nur macht das an einem gewissen Punkt einfach keinen Sinn mehr. Es genügt vielmehr nachvollziehbar zu begründen, dass das, was Molski hier macht, keine Physik ist. Es ist einfach nur Pseudophysik.
Viele Grüße
Ich hielt diese Arbeit allen Ernstes zunächst für einen Aprilscherz.
Das konnte doch nicht ernst gemeint sein, ausgerechnet den Parameter zur Grundlage einer Theorie heranzuziehen, der nirgendwo auch nur einer Randbemerkung Wert gewesen ist. Weder Hahnemann in seinem Organon noch die gegenwärtigen Hersteller auf ihren Webseiten beschreiben, dass irgendeine Form von Zeitmanagement bei der Verschüttelung zu beachten wäre.
Man könnte ebenso für einen Durchschnittssäufer eine mehr oder weniger konstante Zykluszeit für ein Bier feststellen und dann die Molski-Betrachtungen für den Gesamtprozess des Besäufnisses anstellen, was zu denselben Gleichungen führen müsste. Quintessenz: Der Grad der Trunkenheit wäre dann alleine davon abhängig, wie lange man im Wirtshaus sitzt.
Nur das Datum der Veröffentlichung im Oktober ließ mich an der Annahme eines Aprilscherzes zweifeln…
Vielen Dank für die ausführliche Kritik zu diesem Artikel.
Die Zeitschrift Homeopathy liefert mit schöner Regelmäßigkeit Artikel, die auf die physikalischen oder chemischen Grundlagen der Homöopathie eingehen wollen. Die diskutierte, rein theoretische Arbeit ist leider ein typisches Beispiel:
Mit einigem Aufwand wird ein Gedankengang aufgebaut, der kompliziert und wissenschaftlich aussieht, vor Fachbegriffen strotzt, vermutlich aber von den wenigsten Lesern der Zeitschrift nachvollzogen werden kann. Die Schlussfolgerungen sind aber bei weitem nicht so zwingend wie dargestellt. Sie sind nicht mehr als die persönliche Meinung des Autors, an keiner Stelle folgt der nächste Schritt plausibel begründet aus dem Vorherigen. Mehr als vage Analogien hat das Paper nicht zu bieten: „A sieht entfernt aus wie eine bestimmte Eigenschaft von B, also sind A und B fundamental das Gleiche…“
Dem ist noch hinzuzufügen, dass Molski sich für seine Analogie ordentlich anstrengen muss. Denn im Gegensatz zur einfachen ersten Gleichung (1, für die Abnahme der Konzentration des Wirkstoffs in Folge des homöopathischen Potenzierens), die physikalisch einleuchtend hergeleitet wird, folgt die wesentlich komplexere zweite Gleichung (2) aus einem Taschenspielertrick – es wird praktisch versteckt, dass (1) schon „die“ Lösung ist! (1) ist eine gewöhnliche Funktion und eine von mehreren möglichen Lösungen von (2), einer Differentialgleichung zweiter Ordnung. Demzufolge hat man mit (2) also auch mehr Freiheiten zum weiteren Assoziieren. Und erst diese Zweite Gleichung erinnert Molski an das Hulthèn-Potential, das er als Ausgangspunkt für weitere Spekulation nimmt. In anderen Worten, man kann Gleichung (1) zu (2) verkomplizieren. Man muss es aber nicht, im Artikel wird dafür auch kein Grund genannt. An anderen Stellen der Arbeit geht der Autor ähnlich vor.
Pingback: Homöopathie im Deutschen Museum – jetzt wird’s peinlich @ gwup | die skeptiker
Erst Schwache Quantentheorie, jetzt Quasi-Quantum Model of Potentization, es beginnen die Benennungen der Pseudoerklärungen sich so schnell zu ändern wie die der Paramedizin (komplementär, alterna- & integrativ etc).
Der Name ließe sich übrigens zu QuQuMP akronymisieren, was vielleicht erklärt, warum das paper so eine Gurke ist.
Schöner Text, überzeugender Verriß.