„Wie muss man sich signifikante Ergebnisse bei Homöopathiestudien so vorstellen? Wie sieht das denn bei wirksamen Arzneimitteln aus, z.B. Aspirin?“
Das war sinngemäß die Frage des Users 2xhinschauen auf dem GWUP-Blog (Link).
Ich nehme dies zum Anlass, mich einmal generell über die Signifikanz auszulassen, wie sie von den Protagonisten der Homöopathie gerne dargestellt wird – was da eigentlich dahinter steht und was der Patient für sich daraus ableiten kann.
Problemstellung
Die Homöopathie ist, glaubt man ihren Protagonisten, bei all ihrer behaupteten Sanftheit und Natürlichkeit eine sehr wirkungsvolle Therapieform, mit der alle nur erdenklichen Krankheiten und Beschwerden effektiv geheilt werden können. Das gilt angeblich auch für schwerste Pathologien (Krebs, Diabetes, Infektionskrankheiten etc.), insbesondere, wenn sie chronisch sind und die Patienten bereits ‚von der Universitätsmedizin aufgegeben wurden‘. (Anmerkung: Ärzte werden ausschließlich an Universitäten ausgebildet. Nur Heilpraktiker durchlaufen – wenn überhaupt – eine ‚Schule‘.) Kurzum, wer sich der Homöopathie anvertraut, und das tun ja angeblich immer mehr Menschen, wird mit ziemlicher Sicherheit eine durchgreifende Besserung seiner Situation erreichen können – so die vollmundigen Aussagen der Homöopathen jedenfalls.
Was kann der Patient für sich daraus ableiten, wenn ihm erklärt wird, für seine Indikation oder sogar für die Homöopathie als Ganzes gäbe es Studien mit signifikanten positiven Effekten? Studien, in denen also ermittelt wurde, dass das Homöopathikum ’signifikant‘ wirksamer war als das in der Kontrollgruppe verabreichte wirkstofffreie Placebo? Dies wird im ersten Teil dieses Artikels behandelt.
Welche Kennzahl beschreibt hingegen die Erfolgschancen eines Patienten, das heißt, wie stark die Verbesserung eigentlich sein wird, die der Patient von der Behandlung erwarten kann? Wird eine solche Kennzahl überhaupt in Studien oder sonstwo systematisch ermittelt? Gedanken hierzu werden in Kürze in Teil 2 folgen.
Ich kann die obige Frage allerdings nur zum Teil beantworten, denn ich habe mich nur mit Studien zur Homöopathie beschäftigt. Ich befürchte allerdings, dass es bei den evidenzbasierten Kollegen um keinen Deut besser aussieht – schließlich ist auch hier viel Geld involviert. Aber dies macht die Situation bei der Alternativmedizin nicht besser.
Dreh- und Angelpunkt: Signifikante Ergebnisse
Jeder, der sich mit Studien zur Wirksamkeit von Therapien beschäftigt, dürfte davon gehört haben, dass die Ergebnisse ’signifikant‘ sein müssen, um bedeutsam zu sein. Ist das Ergebnis ’signifikant‘, dann gilt die Studie fürderhin als Beleg für eine Wirksamkeit der untersuchten Arznei. Sind sie es nicht, dann gilt der Nachweis als misslungen – was übrigens nicht bedeutet, dass damit das Gegenteil nachgewiesen sei.
Mit signifikanten Vorteilen einer Therapie wird gerne geworben, denn der Laie versteht dem allgemeinen Sprachgebrauch folgend darunter etwas Großes, Deutliches. Ganz im Sinne des Dudens, der die Adjektive ‚bedeutend, bemerkenswert, beträchtlich, deutlich, gewichtig etc.‘ als Synonyme für ’signifikant‘ aufführt (Link).
Diese Sichtweise ist aber nur bedingt zutreffend, denn im Zusammenhang mit Forschungsarbeiten ist die ’statistische Signifikanz‘ gemeint. Diese steht nicht für die Größe eines Unterschiedes zwischen Placebo- und Verumgruppe, sondern für dessen Wahrscheinlichkeit des Auftretens. Üblicherweise wird ein Signifikanzniveau von 5 % als Grenzwert definiert.
Von welcher Wahrscheinlichkeit sprechen wir hier?
Beim Werfen einer idealen Münze ist es gleich wahrscheinlich, ob das Wappen oder die Zahl sichtbar ist, wenn die Münze gefallen ist. Nun ist aber nicht zu erwarten, dass in jedem Fall, beispielsweise nach hundert Würfen, Wappen und Zahl jeweils absolut gleich oft gefallen sein werden. Nehmen wir an, bei 100 Würfen gab es 60 Mal Wappen und 40 Mal Zahl. Ist das noch die zu erwartende zufällige Streuung oder deutet das schon darauf hin, dass die Münze systematisch eine Seite bevorzugt? Hierzu wird mit einem statistischen Testverfahren die Wahrscheinlichkeit berechnet, mit der dieses Ergebnis auftritt, wenn die Münze tatsächlich absolut ‚gleichmäßig‘ wäre. Liegt diese Wahrscheinlichkeit bei unter 5 %, dann gilt die Abweichung definitionsgemäß als signifikant, das heißt, man geht davon aus, dass die Münze wahrscheinlich nicht ‚gleichmäßig‘, sondern eher ‚einseitig‘ ist.
Die Grenze der Signifikanz als Wahrscheinlichkeit von 5 % für das Eintreten des Ergebnisses von 5 % bedeutet aber auch, dass es durchaus Fälle gibt, in denen zwar tatsächlich ein Zufallsergebnis vorliegt, dies aber, weil es wenig wahrscheinlich ist, als ein Nicht-Zufallsergebnis gedeutet wird. Dies nennt man einen ‚Fehler 1. Art‘, ‚Alpha-Fehler‘ oder ein ‚falsch-positives Ergebnis‘. Im Beispiel bedeutet dies, dass man die Münze für einseitig hält, sie es in Wirklichkeit aber nicht ist. Es dürfte klar sein, dass ein tatsächlich falsch-positives Ergebnis bei einer Wiederholung des Experiments aufgrund der geringen Wahrscheinlichkeit (sehr wahrscheinlich) nicht mehr auftritt.
Naheliegend wäre nun, einfach die Grenze von 5 % auf kleinere Werte zu verschieben. Dies erhöht aber das Risiko, dass man ein tatsächlich nicht auf einem Zufall beruhendes Ergebnis nicht erkennt. Etwa, dass die Münze tatsächlich eine Seite bevorzugt, allerdings nur in geringem Umfang. Dies ist dann der ‚Fehler 2. Art‘, ‚Beta-Fehler‘ oder ein ‚falsch-negatives Ergebnis‘. Im Beispiel käme man zu dem Schluss, die Münze wäre in Ordnung, sie ist es aber in Wirklichkeit nicht. Auch ein solcher Fehler ließe sich durch Wiederholung des Versuchs (wahrscheinlich) erkennen.
Üblicherweise soll die Wahrscheinlichkeit eines Fehlers 2. Art bei nicht mehr als 20% liegen, was unter Anderem durch die Anzahl der Testwürfe – 1000 anstatt 100 – und die Anwendung eines geeigneten Testverfahrens sichergestellt wird. Damit wollen wir uns aber hier nicht befassen.
Bei einer klinischen Studie wird aber nicht gewürfelt oder eine Münze geworfen – hoffentlich nicht! Der Zufall kommt auf andere Weise ins Spiel. Bekanntlich werden die Testpersonen in zwei Gruppen aufgeteilt, deren eine das zu testende Mittel erhält (‚Verum‘), die andere zu Vergleichszwecken ein Mittel ohne jeden Wirkstoffgehalt. Wenn sich nach der Therapie zeigt, dass es in beiden Gruppen unterschiedlich starke Verbesserungen gegeben hat, dann ist die Frage, ob dies vielleicht auch nur eine Folge einer zufälligen ungleichmäßigen Verteilung der Patienten gewesen sein könnte. Es könnte ja sein, dass sich bei allen geheilten Probanden die Besserung ohne den Einfluss des Mittels ergeben hat, diese Patienten jedoch unterschiedlich auf die beiden Gruppen verteilt worden sind. Dies würde wie ein Vorteil für eine der beiden Gruppen aussehen, jedoch auf einem Zufall beruhen.
Mit statistischen Testverfahren, die an die Art der vorliegenden Daten angepasst sind, wird ermittelt, wie wahrscheinlich eine solche Ungleichmäßigkeit der Verteilung wäre, wenn sie nur durch die zufällige Verteilung zustande gekommen wäre und das Mittel nicht wirksam war. Ist diese Wahrscheinlichkeit geringer als 5 %, dann geht man davon aus, dass der Unterschied signifikant dafür ist, dass die Wirkung des eingenommenen Mittels als Ursache angesehen werden kann. Die Einschränkungen zu falsch-positiven und falsch-negativen Ergebnissen gelten auch hier wie oben beschrieben.
Die solide Vorgehensweise
Ein solides wissenschaftliches Vorgehen sieht etwa wie folgt aus:
Man legt vorher fest, also bevor man die Untersuchung startet, anhand welcher Daten man den Nachweis führen will, wie man sie ermitteln und auswerten will. Will man eine erfolgreiche Therapie beurteilen, indem man die Schwere der Symptome bewertet, die Dauer der Beschwerden, irgendwelche messbaren Daten, die Körpertemperatur vielleicht oder das subjektive Wohlbefinden? Gleichgültig was es ist, woran man den Erfolg erkennen will, man muss dies vor Beginn der Studie festlegen. Der Königsweg ist, die Studie vorher registrieren zu lassen oder eine Veröffentlichung zu schreiben, in der diese Festlegungen getroffen werden. In der Münchner Kopfschmerzstudie ist man so verfahren [1] oder auch bei der Metaanalyse von Mathie [2].
Woher weiß man nun, welches Kriterium man verwenden soll? Zweckmäßigerweise natürlich das, was man am einfachsten messen kann oder das die deutlichsten Ergebnisse erzielt. Wenn man keine Literaturdaten oder Vorarbeiten anderer Autoren zur Verfügung hat, dann macht man eine Pilotstudie mit einer relativ kleinen Teilnehmerzahl und probiert das Vorhaben einfach aus. Anhand dieser Vorstudie, die auch veröffentlicht wird, trifft man die Festlegungen für die nun folgende Hauptstudie. In dieser Hauptstudie ergibt sich dann im Idealfall tatsächlich ein signifikanter Unterschied der Arznei gegenüber Placebo. Damit ist man dann schon auf einer sehr hohen Stufe der Evidenz angekommen – die nur noch dadurch übertroffen werden kann, dass andere Forscher unabhängig von der ersten Forschergruppe bei vergleichbaren Versuchen zu ähnlichen Ergebnissen kommen und dies in einer Metaanalyse zusammenfassend bestätigt werden kann.
Soweit der Idealfall.
Die Zitier-Signifikanz
Der Idealfall des Nachweises ist, wie vielleicht nachvollziehbar, recht aufwändig – und trägt auch immer das Risiko des Scheiterns in sich. Da muss man sich schon überlegen, was man eigentlich will:
Es ist werbewirksam, wenn man auf signifikante Studien verweisen kann, was der Laie fälschlicherweise aber durchaus erwünscht als einen fühlbaren großen Vorteil versteht, den er bei Anwendung der Therapie erreichen kann. Es müssen also signifikante Studienergebnisse her! Also irgendwo muss in der Studie das Wort ’signifikant‘ auftauchen, sonst kann man es nicht zitieren. Natürlich wäre es schön, wenn man Ergebnisse hätte, deren Signifikanz über jeden Zweifel erhaben sind – aber was macht man, wenn das nicht der Fall ist?
Möglichkeit 1: Cherrypicking
Wenn man eine Studie unternimmt, dann kann man einfach sehr viele Vergleichsdaten ermitteln (‚Data mining‘). Da die Signifikanz mit einer Wahrscheinlichkeit von 5 % auftritt, wird man bei hinreichend großer Anzahl von Daten auch etwas finden können, das signifikant ist. Und schon hat man ein zitierfähiges signifikantes Ergebnis erzeugt. Natürlich ist das kein wissenschaftlich solides Vorgehen, siehe oben, aber dennoch legen manche Arbeiten den Schluss nahe, dass so etwas passiert.
In der Arbeit von Ferley et al. geht es beispielsweise um die Wirksamkeit eines homöopathischen Präparats namens Oscillococcinum bei grippalen Infekten [3]. Eine ausführliche Besprechung dieser Arbeit findet sich in meinem Buch (Link), eine Replikation durch Papp et al. wurde hier in meinem Blog besprochen. Eine Vorstudie wurde nicht veröffentlicht, die Studie wurde auch nicht registriert, was zur Zeit der Veröffentlichung allerdings auch noch nicht üblich war.
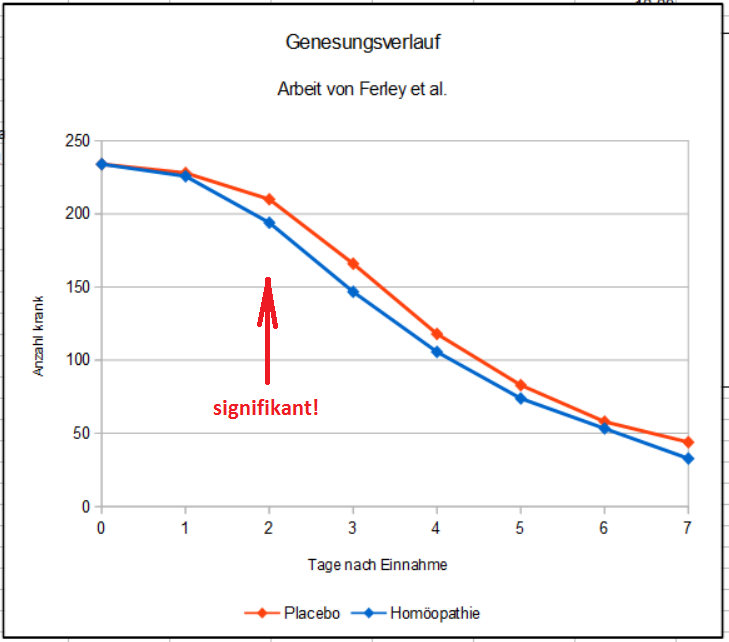
Es ging also um ganz banale Erkältungskrankheiten, die normalerweise innerhalb etwa einer Woche, maximal in zwei Wochen, von selbst ausheilen. Jetzt müssen wir uns vorstellen, dass die Forscher vorab, also bevor die Daten erhoben wurden, festgelegt haben, dass sie die Wirkung des Mittels anhand der Genesungsrate nach zwei Tagen beurteilen wollen. So haben sie es jedenfalls in der Studie beschrieben. Sie wollen also nicht die durchschnittliche Dauer bei allen Patienten zur Bewertung heranziehen, sondern nur abzählen, wie viele Patienten am Ende des zweiten Tages – also weit vor dem ’normalen‘ Ende der Beschwerden – keine Symptome mehr haben. Klingt zunächst ungewöhnlich, könnte aber durchaus aus der Überzeugung geboren sein, dass das verabreichte Medikament eine richtige Bombe ist. Man könnte allerdings auch die Frage stellen, ob diese Patienten überhaupt an einer soliden Erkältung erkrankt waren.
Und, siehe da, es zeigt sich, dass tatsächlich am zweiten Tag ein statistisch signifikanter Unterschied in den Genesungsraten vorliegt. Also tatsächlich das Power-Medikament, wie angenommen? Im Zitat in der Ratgeberliteratur liest sich das dann so:
„Eine interessante Doppelblindstudie mit einer sehr hohen Teilnehmerzahl (…) konnte zeigen, dass das homöopathische Mittel Oscillococcinum (…) die Zahl der Genesungen innerhalb der ersten 48 Stunden im Vergleich zur Placebogruppe signifikant erhöhte“ [4, S. 45]
Was der Laie gerne so versteht, dass ab dem zweiten Tag ein Vorteil bestanden hätte.
Ein einfacher Test, ob tatsächlich ein Cherrypicking vorgelegen haben könnte, besteht darin, anhand des Textes der Studie zu prüfen, welche Signifikanz sich bei einem geringfügig geänderten Bewertungskriterium ergeben hätte. Hier vielleicht bei einem anderen Zeitpunkt, also nicht nach zwei Tagen, sondern nach drei Tagen. Und tatsächlich, da ergibt sich eben keine Signifikanz mehr! Auch nicht nach nur einem Tag oder überhaupt in den Genesungsraten irgendeines anderen Tages während der Studie. Nur an dem einen eigentlich völlig unlogisch festgelegten Stichtag zeigt sich ein signifikantes Ergebnis, sonst nicht.
Dies ist der Heilungsverlauf der beiden Gruppen aus Ferleys Arbeit, allerdings auf gleiche Gruppenstärken umgerechnet.
In Summe zeigt sich, dass der Effekt des Homöopathikums eher gering ist. Aus welchen Zufällen heraus auch immer: genau an dem einen Tag, den die Autoren völlig unlogisch als Bewertungszeitpunkt ausgesucht hatten, hatte sich ein signifikanter Wert gezeigt. Der obige Text des Ratgebers müsste anders lauten:
Der signifikante Vorteil für den Patienten besteht nicht ab dem zweiten Tag, sondern nur am zweiten Tag. Wir werden die Daten später noch genauer betrachten.
Möglichkeit 2: Man nehme etwas anderes Signifikantes
Wenn sich nun beim besten Willen kein signifikanter Unterschied zwischen den beiden Gruppen finden lässt, dann kann man auch andere Daten nehmen, um aus ihnen ein signifikantes Ergebnis zu erzeugen. Ein Beispiel ist die Arbeit von Cavalcanti et al. [5]. Hier geht es um die Behandlung des Juckreizes, der bei Dialysepatienten auftreten kann. In beiden Gruppen, Homöopathie und Placebo, traten Verbesserungen auf, in der Homöopathiegruppe durchaus stärkere Effekte als unter Placebo, aber es reichte eben nicht für einen signifikanten Unterschied.
Die Lösung: Zu den Bewertungstagen führt man nicht nur einen Vergleich zwischen den Gruppen aus, sondern auch zwischen den am Ende der Behandlung ermittelten Daten und denen am Anfang. Siehe da: In der Homöopathiegruppe zeigen sich signifikante Unterschiede, in der Placebogruppe nicht. In der Zusammenfassung steht dann:
„Reduction was statistically significant (P < 0.05) at every point of the observation“
Wem fällt auf, dass da die Wörter ‚compared to placebo‘ fehlen?
Was sagt das in dieser Form aus?
Nichts.
Was bedeutet es, wenn die Veränderungen in der Gruppe signifikant sind, also wahrscheinlich nicht zufälliger Natur sind? Nichts. Die Unterschiede sind zu beiden Zeitpunkten für jeweils alle Gruppenmitglieder gemessen worden und liegen nach Maß und Zahl vor. Eine Unsicherheit besteht hinsichtlich möglicher Messfehler, aber die kann man nicht mit einem Signifikanztest ermitteln.
Ebenso wenig kann man damit unterscheiden, welche Ursache zur Verbesserung der Situation geführt hat, ob diese tatsächlich durch das Medikament bewirkt wurden oder von irgendwelchen äußeren Einflüssen. Die kann man mit einer Kontrollgruppe erfassen – aber für diesen Gruppenvergleich ergab sich ja gerade kein signifikanter Unterschied. Ob die Entwicklung ein Zufall war oder nicht, könnte man eher dadurch klären, dass es (a) eine plausible Erklärung für die Ursachen gibt, die die Entwicklung in Gang gesetzt haben und (b) dass äußere Einflüsse ausgeschlossen werden können.
Aus dieser Betrachtung folgt, dass es ziemlich genau auf den Wortlaut ankommt, mit dem die Forscher ihr Ergebnis beschreiben, um entscheiden zu können, ob es sich um eine sinnvolle Angabe handelt (’signifikante Verbesserungen in der Verumgruppe im Vergleich zur Kontrollgruppe‘) oder eben nicht (’signifikante Verbesserungen in der Verumgruppe‘). Dazu wird man sich am besten ebenfalls die Originalveröffentlichung vornehmen, denn eventuell ist die Zusammenfassung nicht so deutlich formuliert, wie sie es sein sollte.
Möglichkeit 3: Finde den Trend
Wenn man nun beim besten Willen nichts findet, was signifikant ist, was macht man dann mit der schönen und teuren Studie? Dann wird man ja doch wohl noch irgendwo einen Trend finden können, also einen Unterschied zwischen Homöopathie und Placebo zugunsten Homöopathie. Auch wenn der dann nicht signifikant ist, kann man immer noch von einem Trend zugunsten der Homöopathie sprechen. Klingt ja auch gut, wie zum Beispiel in der Pressemeldung zur Preisverleihung für die Meta-Analyse von Rumpl (s. hier).
Aber was bedeutet das wirklich?
Signifikanz ist ein Maßstab dafür, ob ein festgestellter Unterschied zwischen den zwei Gruppen wahrscheinlich auf einem Zufall beruht oder nicht. Ist ein Ergebnis nicht signifikant, dann kann es sein, dass der Unterschied auf der Verteilung der Patienten auf die Gruppen beruht – und rein gar nichts mit einer Wirkung des Mittels zu tun hat.
Natürlich ist es möglich, dass nur ein kleiner Effekt aufgetreten ist, der einfach nur nicht groß genug war, um als signifikant in Erscheinung zu treten. Sofern es keine auf plausiblen Annahmen und bekannten Effekten beruhende Erklärung für einen Effekt gibt – wie es bei der Homöopathie ja der Fall ist – dann gibt es eigentlich nur einen sinnvollen Weg, herauszufinden, ob es sich tatsächlich um einen zwar kleinen aber nicht-zufälligen Effekt handelt, nämlich den Versuch zu wiederholen, gegebenenfalls sogar mit einer höheren Teilnehmerzahl. Ein tatsächlich vorhandener Effekt wird sich dann erneut zeigen, in der gemeinsamen Betrachtung der Ergebnisse (Metaanalyse) müsste sich der Effekt deutlicher identifizieren lassen – und irgendwann auch als signifikantes Ergebnis feststellbar sein.
Alleine aus einem für die Homöopathie positiven Ergebnis zu schließen, dass es sich hierbei um einen – natürlich auf die Wirksamkeit des Mittels zurückgehenden – Trend handele, ist nach meiner Meinung Humbug. Der Rückschluss auf die Wirksamkeit ist wegen eines möglichen Fehlers erster Art schon bei einem signifikanten Ergebnis aus nur einer einzigen Studie nicht unbedingt gerechtfertigt – um wie viel mehr erst, wenn keine Signifikanz gegeben ist.
Zahlenwerte zur Signifikanz
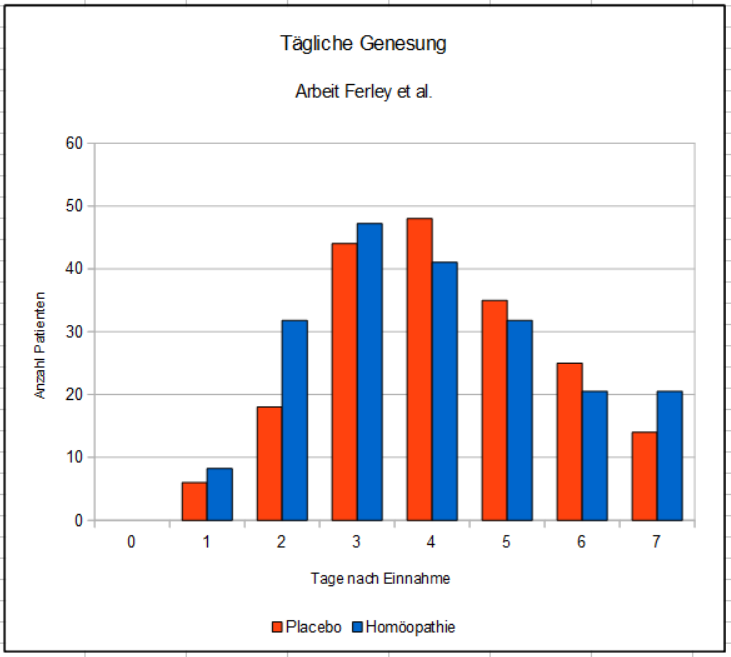
Um einige Aspekte der Zahlenwerte zu beleuchten, sei hier als Beispiel das Ergebnis aus der Arbeit von Ferley et al. betrachtet, die Arbeit, die auch schon oben zitiert wurde. Wir betrachten hier aber die Daten zur Krankheitsdauer aller Patienten, wie sie aus den Angaben der Studie errechnet werden können. Der Einfachheit halber lassen wir für diese Betrachtung die Patienten weg, die innerhalb der Beobachtungszeit von sieben Tagen nicht gesund wurden. Dies ergibt die Verteilung im nächsten Bild.
Dies ist die originale Verteilung, wie sie aus Ferleys Daten errechnet werden kann. Man erkennt die höhere Anzahl der Patienten, die am zweiten Tag nach der Einnahme in der Homöopathiegruppe geheilt waren. Die statistischen Daten lauten:
| Homöopathie | Placebo | |
|---|---|---|
| Anzahl Teilnehmer | 196 | 190 |
| Mittlere Dauer (Tage) | 3,99 | 4,27 |
| Standardabweichung | 1,65 | 1,45 |
Im Klartext bedeutet dies, dass in der Homöopathiegruppe die Beschwerden im Durchschnitt 0,28 Tage kürzer andauerten als mit Placebo (das sind nur knapp 7 Stunden!). Man könnte aus dem Diagramm auch ablesen, dass nur 17 Patienten einen Vorteil hatten. Dies ist die Differenz zwischen den an den Tagen 1 bis 3 genesenen Patienten in der Homöopathiegruppe zur Placebogruppe. Bezogen auf die Anzahl der Patienten, die das homöopathische Mittel einnahmen, sind dies 8,5 % – also nur knapp einer von zehn Patienten. Mehr als neun von zehn Patienten werfen ihr Geld zum Fenster hinaus. In Anbetracht der üblicherweise vollmundigen Aussagen zur Wirksamkeit der Homöopathie in allen Lebenslagen erscheint mir dieses Ergebnis äußerst kümmerlich.
Nach meiner Rechnung zeigt ein sogenannter T-Test mit diesen Daten, dass dieser Unterschied nicht signifikant ist (Wahrscheinlichkeit p = 0,08).
Hätte Ferley aber prozentual das gleiche Ergebnis mit einer höheren Anzahl von Patienten erreicht, dann sähe das ganz anders aus: Bei einer um die Hälfte höheren Teilnehmerzahl also bei 294 Homöopathie- und 285 Placebopatienten hätte sich bei der absolut gleichen prozentualen Verteilung ein signifikantes Ergebnis ergeben (p = 0,03). Dies liegt daran, dass durch die höhere Anzahl die Verteilung sicherer bekannt ist und man davon ausgeht, dass die wahren Werte besser, das heißt mit kleinerem Fehler, abgebildet werden.
Also: Auch ein solch kleiner Vorteil kann signifikant sein, wenn er mit einer hinreichend großen Zahl an Versuchspersonen ermittelt worden ist. Die dem Laien naheliegende Schlussfolgerung ’signifikant = groß‘ ist also unzutreffend. Natürlich wäre in jedem Versuch ein nicht signifikanter Unterschied kleiner als ein signifikanter, allerdings ist das nur ein relativer Maßstab, kein absoluter. Genau genommen ist die Aussage, die oftmals als Qualitätsmerkmal zitiert wird (‚Ergebnis eine Großen Studie mit vielen Teilnehmern‘), eher ein Hinweis auf das Gegenteil, nämlich dass die Gruppenunterschiede nur recht gering sind.
Quintessenz:
Ob ein Ergebnis statistisch signifikant ist oder nicht, sagt nichts darüber aus, wie groß der Nutzeffekt für den Patienten ist. Liegt dem Versuch eine hohe Anzahl der Teilnehmer zugrunde, dann kann es sich auch um vergleichsweise unbedeutende Effekte handeln, mit denen eine Signifikanz zu erreichen ist.
Mit Fug und Recht kann ein Patient erwarten, dass ein ‚richtiges‘ Medikament signifikant besser wirkt als ein Placebo. Das sollte ein Selbstverständlichkeit sein, kein Werbeargument. Als solches taugt die Aussage nämlich nicht, weil überhaupt nicht erkennbar ist, wie stark denn der Nutzen des Medikaments für den Patienten ist. Genau genommen ist das Werbeargument der signifikanten Studienergebnisse etwa gleich stark wie bei einem Auto der Hinweis, dass es vier Räder hat. Oder dass ein neu errichtetes Gebäude stehen bleibt und nicht einstürzt.
Eine Selbstverständlichkeit eben.
Literaturquellen
[1] Walach H, Haeusler W, Lowes T, Mussbach D, Schamell U, Springer W, Stritzl G, Gaus W, Haag G: Classical homeopathic treatment of chronic headaches, in: Cephalalgia 1997; 17:119-126, Link zum Abstract
[2] Mathie RT, Lloyd SM, Legg LA, Clausen J, Moss S, Davidson JRT, Ford I: Randomised placebo-controlled trials of individualised homeopathic treatment: systematic review and meta-analysis, in: Systematic Reviews 2014, 3: 142, doi: 10.1186/2046-4053-3-142, Link zum Volltext
[3] Ferley JP, Tmirou D, D’Adhemar D, Balducci F: A Controlled Evaluation of a Homeopathic Preparation in the Treatment of Influenza-Like Syndromes‘ in: British Journal of Clinical Pharmacology 1989; 27: 329 – 335, Link zum Volltext
[4] Sommer S.: Homöopathie – warum und wie sie wirkt, Mankau Verlag, Murnau, 2011
[5] Cavalcanti, A. M. S., et al. „Effects of homeopathic treatment on pruritus of haemodialysis patients: a randomised placebo-controlled double-blind trial.“ Homeopathy 92.4 (2003): 177-181. Link zum Abstract








Alle sprechen hier ja noch (optimistisch) von ‚Studien‘, wobei dann davon ausgegangen werden müsste, dass es nur eine abhängige Variable pro Studie gibt, damit die obigen Berechnungen stimmen, aber die Sache ist doch noch dramtischer: In der Regel werden ja wohl mehrere (wenn nicht dutzende) AVn appliziert und dann geschaut wo etwas signifikant wird, typisches p-hacking, also noch mal eine Verschäfung des oben genannten Cherrypickings.
Und das ist leider nicht nur ein Problem der Alternativmedizin, sondern scheint mir im Moment eher ein generelleres zu sein, was auch in anderen Wissenschaftszweigen auftritt (vgl. Simmons et al 2011 – False positive Psychology). Macht die Ergebnisse der Homöopathen aber auch nicht besser….
Wie wäre das ’statistisch richtig‘ auszuwerten?
Hallo,
ich selbst bin auch sehr kritisch gegenüber Homöopathie eingestellt, aber dieser Artikel gefällt mir überhaupt nicht. Wenn man so ein Ergebnis schon statistisch auswerten möchte, sollte man dies richtig machen.
Im Artikel geschieht das nur sehr oberflächlich, da habe ich mir mehr erhofft.
Beste Grüße
Michael
Pingback: Homöopathische Quanten: Verschränkt oder beschränkt? @ gwup | die skeptiker
Pingback: Was Sie über die Homöopathie wirklich wissen sollten… Teil 3.3 |
Pingback: Erstes Strategietreffen der Homöopathiekritiker am letzten Januar-Wochenende in Freiburg @ gwup | die skeptiker
@Harry_X
>> Verunsicherung, was man glauben kann und was eben nicht
Ja und das ist gut nachvollziehbar und verständlich und geht jedem immer wieder so.
Ich riskiere jetzt mal etwas Wortklauberei (glauben vs. vertrauen) oder von mir aus Klug$%&#rei… denn 1. eigentlich soll man sowieso gar nichts „glauben“, denn 2. funktioniert Wissenschaft auch, wenn man nicht an sie glaubt. Nur dass sich auch in der Wissenschaft die Leute anscheinend dauernd widersprechen und das ja auch nur Menschen sind – mit Budgetsorgen, Jobängsten, Machtwillen, Rechthaberei usw.
Der Punkt ist, dass man nicht von jedem Fach (Geldanlage, Fußball, Sicherheitspolitik, Medizin…) genug für eine eigenständige Meinung wissen und verstehen kann, auch wenn viele Leute das bei genau den genannten Themen nie zugeben würden. Entweder man fuchst sich in ein Thema hinein oder man man muss jemand vertrauen.
Nur dass Vertrauen fundierter und rationaler ist (sein sollte) als Glaube und auch erschüttert und wieder entzogen werden kann. Glauben meistens nicht. Es ist schon ein Unterschied da, aber den muss jede/r erstmal für sich selber machen.
Glaube ich an meinen Börsenguru oder vertraue ich ihm? Meinem Heilpraktiker? Dem Dorftrainer unserer D-Jugend?
Sorry für ein bisschen Fundamentaltrivialität zum Feierabend 😉
Herr Aust, danke für die Klarifikation. Das war mir so bisher nicht bewußt geworden.
Ich denke, viel zu oft wird sich auf „allgemeines Wissen“ berufen, was bei näherer Betrachtung der Überprüfung nicht stand hält – einfach, weil man als Einzelner natürlich nicht alles einzeln überprüfen kann und dann von „Experten-Aussagen“ abhängig ist, bei denen man nicht unterscheiden kann, ob sie eine reelle Auskunft erteilt haben oder einen nur um die schnelle Mark erleichtern wollten (zB „Reifengas“).
Bei mir persönlich führt all das eher zu einer mehr oder minder stark andauernden Verunsicherung, was man glauben kann und was eben nicht.
@ Harry_X
„Ansonsten wäre ja jede einzelne Studie von sehr geringem Wert“
Ja und nein.
Es ist tatsächlich so, dass eine einzelne Studie trotz eines signifikanten Ergebnisses wenig bis nichts aussagt. Es gibt die Wahrscheinlichkeit von 5 % dass ein Zufallsergebnis aussieht wie ein signifikantes Resultat, wobei man noch nicht einmal weiß, wie oft diese Untersuchung schon gemacht wurde, jedoch wegen eines nicht erwünschten Ergebnisses nicht veröffentlicht wurde (Publication bias, Schubladenproblem).
Eine Studie kann aber einen Baustein zum wissenschaftlichen Nachweis liefern, etwa wenn sie unabhängig erfolgreich repliziert worden ist, am besten noch mehrfach von unterschiedlichen Teams an verschiedenen Orten. Alternativ könnte Die einzelne Studie jedoch auch in ein ganzes Programm eingebunden sein, wie bei der regulären Zulassung von Arzneimitteln. Dort wird die prinzipielle Wirksamkeit des Mittels in den Phasen 0 bis II erforscht, wenn diese erfolgreich verlaufen sind, dann werden mit dem fertigen Medikament auch klinische Studien zum Wirksamkeitsnachweis durchgeführt (Phase III). Prinzipiell genügt hier eine Studie, sofern hinreichend groß.
Anders ausgedrückt: Ist eine Wirksamkeit aus anderen Gründen hinreichend wahrscheinlich (‚a-priori-Wahrscheinlichkeit‘), sei es aus anderen Studien, Voruntersuchungen oder infolge einer gute gesicherten Theorie, dann ist eine klinischen Studie durchaus wichtig als finaler Nachweis. Gibt es diese Wahrscheinlichkeit nicht – dann brint eine einzelne Studie in der Tat nicht viel.
Die Wirksamkeit der Homöopathie als Ganzes dadurch nachweisen zu wollen, dass man die verschiedensten Studien zu unterschiedlichen Beschwerden zusammenfasst und statistisch auswertet, halte ich allerdings für faulen Zauber. Siehe auch diesen Artikel hier:
http://www.beweisaufnahme-homoeopathie.de/?page_id=2299
Äh, ja … Danke 🙂
So sollte es eigentlich sein. wenn wenigstens der OK ist, bin ich ja froh. 😉
äh ja. Aber dieser Fehler war ja trivial aufzuspüren.
Wenn ich 100x die gleiche Studie mit Zufallsdaten machen würde, erhalte ich 5x eine, die signifikant ist.
Aber bei 100 beliebigen Studien (also aus verschiedenen Feldern) kann ich doch nicht. Oder doch?
Jedenfalls habe ich es so verstanden…
Ansonsten wäre ja jede einzelne Studie von sehr geringem Wert, oder nicht?
… irgendwie bin ich ja froh, dass solche Pannen nicht nur mir passieren …
Äh.
Wenn ich 100 mal eine Studie durchführe deren Ergebnisse rein zufällige Daten sind, erhalte ich — rein statistisch betrachtet — trotzdem in ungefähr 20 (5% von 100) Fällen ein Signifikantes Ergebnis.
Streng genommen sind 20 von 100 aber 20 %.
Gemeint war bestimmt: Man bekommt in jeder 20. Studie ein signifikant positives Ergebnis. Also in 5 von 100. Das sind dann auch die 5%…
😉
@Harry_X, 4. Januar 2016 um 08:15:
Wenn man weiß, was p = 0,05 bedeutet ergibt sich das zwangsläufig.
p ist definitionsgemäß die Wahrscheinlichkeit der sogenannten Nullhypothese. Das ist die Annahme, dass die Ergebnisse in einer Studie rein zufällig aufgetreten sind.
Nun hat man sich in der Welt der Wissenschaft einfach darauf geeinigt, ab welchem Wahrscheinlichkeitswert die Nullhypothese als unbewiesen gilt, d.h. ab wann ich davon ausgehen kann, dass meine Ergebnisse eben nicht mehr zufällig sind. Und diese Grenze wurde eben auf diese bekannte Wahrscheinlichkeit von 5% (p = 0,05) Festgesetzt — auch Signifikanzniveau genannt.
Wenn man nun das passende mathematische Modell für sein Studiendesign nimmt, kann man das Signifikanzniveau für seine Ergebnisse ausrechnen.
Und jetzt kommt der Klopper! Wenn ich 100 mal eine Studie durchführe deren Ergebnisse rein zufällige Daten sind, erhalte ich — rein statistisch betrachtet — trotzdem in ungefähr 20 (5% von 100) Fällen ein Signifikantes Ergebnis.
Man kann sich auch mal „https://de.wikipedia.org/wiki/Statistische_Signifikanz“ durchlesen.
Gerade die Frage nach der Relevanz oder der Größe des Therapieeffekts will ich im zweiten Teil behandeln.
Genau das: Ich kann nur zu Homöopathiestudien etwas sagen, medizinische Arbeiten habe ich nicht im erforderlichen Umfang gelesen (und verstanden), dass ich ein allgemeines Urteil über die Arbeitsweise abgeben könnte. Allenfalls sind gewisse Rückschlüsse möglich, die sich daraus ergeben, dass bei den Studien zur Homöopathie das ’normale‘ Instrumentarium benutzt wird – was nicht beinhaltet, WIE diese angewendet werden.
Bonusfrage: Gibt es in der Statistik neben „Signifikanz“ auch den Begriff der „Relevanz“, oder ist Relevanz nur eine Interpretation? Oder die Prämisse? Hintergrund der Frage ist (neben der Notwendigkeit, zwischen Koinzidenz, Korrelation und Kausalität zu unterscheiden, siehe oben bei WolfgangM) eine kurze, aber augenöffnende Diskussion „neulich“ bei Ulrich Berger (http://scienceblogs.de/kritisch-gedacht/2014/10/31/verbreitung-von-unsinn-eine-kritik-der-kritik/). Dort warnte ein namhafter Psychologe (A. Hergovich aus Wien) vor zu großen Stichproben, um das Aufblasen irrelevanter Effekte (meine Wortwahl) in die Signifikanz hinein zu vermeiden. Das Thema kam in deinem Artikel auch vor.
Mir erschien dies widersinnig, denn nicht jeder „signifikante“ Effekt ist auch „relevant“. Für mich war das eher ein Hinweis darauf, dass man (evtl nicht nur in der Psychologie) in numerischen Studienergebnissen gerne noch ein wenig Data Mining macht, um Funde präsentieren zu können, nach denen man gar nicht gesucht hat und für das Studiendesign evtl. gar nicht geeignet war. Je kleiner die Stichprobe, desto eher geht das nicht, stimmt, aber mir scheint das Alternativmedizin für ein Phänomen zu sein, das man besser mit wissenschaftlicher Medizin behandeln sollte 😉
Ich war ein paar Tage nicht hier, gerade erst gesehen: Danke für die Arbeit, das Thema laienverständlich zu erklären. Hab in der Tat was dazugelernt… durch Gigerenzers „Risiko“ war ich ja voraufgeklärt, wie man zahlenmäßige Studienergebnisse lesen sollte und wie besser nicht. Wenn man die Zahlen denn hat. Hier kam jetzt die Skepsis gegenüber der verbalen Zusammenfassung von Studienergebnissen dazu, und dass die Anwendung auf die persönliche Situation eines Patienten nochmal eine Ecke haariger ist, als G. das schon ausgeführt hat (wievielen/wenigen Patienten in absoluten Zahlen hat die getestete Intervention geholfen und wievielen/wenigen hat sie evtl. geschadet, und wie kann ich erkennen, in welche Gruppe ich evtl hineingehöre).
Alles im Artikel Gesagte gilt im übrigen sicher für alle medizinischen Studien, unabhängig vom Untersuchungsgegenstand. Du hast es im Text kurz erwähnt, aber dann nur Homöopathiestudien betrachtet – ich denke mal, weil Du die eben draufhast.
Nochmal danke, freue mich auf Teil 2
„Die statistischen Signifikanz von p=0,05 bedeutet ja auch, dass jede 20 Studie zufällig ein signifikantes Ergebnis ergibt. Es stellt sich daher auch die Frage, ob das Ergebnis plausibel ist.“
Waas? Wie kommt man denn auf sowas??
Die statistischen Signifikanz von p=0,05 bedeutet ja auch, dass jede 20 Studie zufällig ein signifikantes Ergebnis ergibt. Es stellt sich daher auch die Frage, ob das Ergebnis plausibel ist.
Wiegt man je 50 Äpfel zweier Apfelsorten ab, so wird man recht rasch und plausibel herausfinden, welche Sorte schwerere Äpfel hat. So weit so gut.
Aber es ist ja auch bekannt, dass die Klimaerwärmung mit dem Rückgang der Piraten auf den Weltmeeren korreliert- das ist sicher signifikant aber nicht plausibel.
Hochsignifikant ist auch die Korrelation der Zunahme von Autismus in den USA und die Zunahme des Umsatzes biologischer Lebensmittel.
Tyler Vigen hat hier eine Reihe von signifikanten Korrelationen gebracht:
http://tylervigen.com/spurious-correlations
Die Scheidungsrate in Maine korreliert mit dem Margarineverbrauch.
Zusammenfassung: Korrelation bedeutet nicht unbedingt Ursächlichkeit
Aus meiner Praxis kann ich ein kleines Schelmenstück in Sachen „Signifikanz“ und Bedeutung beitragen. Im Rahmen einer teilweise hitzig geführten Diskussion zu einem höchst unplausiblen, alternativen Behandlungsverfahren (Holopathie) wurde mir eine medizinische Doktorarbeit zur Verfügung gestellt, in der besagtes Verfahren untersucht wurde.
Am Fazit der Arbeit kam niemand vorbei: keine statistisch (oder sonstwie) signifikanten Unterschiede zwischen den Placebo- und der Verumgruppen. Der Hersteller wollte aber nicht gelten lassen, dass – wie von den Kritikern aus der Zusammenfassung herausgelesen – überhaupt keine Vorteile festgestellt worden seien.
Und tatsächlich fand sich in der holopathisch behandelten Gruppe im Lauf der Zeit eine statistisch signifikante Verbesserung des Zustandes der (an Polyarthritis leidenden) Patienten. Die Fortschritte in der Placebogruppe waren hingegen statistisch nicht signifikant. Also doch ein Trend für die Holopathie?
Leider nicht, denn bei genauerem Hinsehen waren die Fortschritte in beiden Gruppen sehr ähnlich und wohl gut durch Placebo und normalen Verlauf der Krankheit zu erklären, zumal die Beobachtungsdaten – vor allem Fragen an die Patienten und an die Ärzte – subjektiv und damit für Placebo anfällig waren. Des Rätsels Lösung: In der Verumgruppe gab es doppelt so viele Probanden, so dass der gleiche kleine (aber wohl nicht zufällige) Effekt einmal über und einmal unter der üblichen (aber letztendlich willkürlichen) Schwelle von p=0.05 lag.
Nachzulesen unter http://scienceblogs.de/kritisch-gedacht/2009/03/01/daten-und-fakten-zur-holopathie-ein-gastbeitrag-von-philippe-leick/
Pingback: Keine Lust auf Harmonie? Reden Sie über Homöopathie @ gwup | die skeptiker